S15-05 算法-树结构
[TOC]
树结构 Tree
树
什么是树
真实的树: 相信每个人对现实生活中的树都会非常熟悉。
树的特点:
- 树通常有一个根。连接着根的是树干。
- 树干到上面之后会进行分叉成树枝,树枝还会分叉成更小的树枝。
- 在树枝的最后是叶子。
树的抽象: 专家们对树的结构进行了抽象,发现树可以模拟生活中的很多场景。
模拟树结构
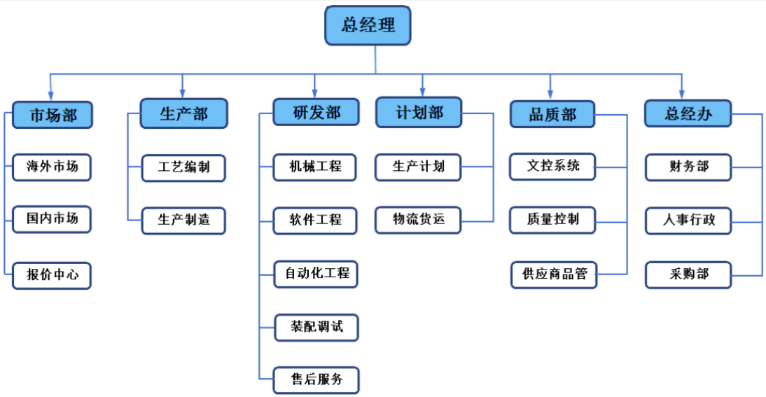
公司组织架构:
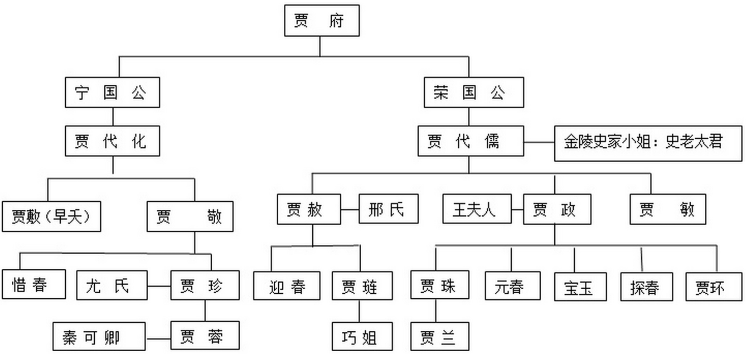
红楼梦家谱:
DOM Tree:

树结构的抽象
我们再将里面的数据移除,仅仅抽象出来结构,那么就是我们要学习的树结构
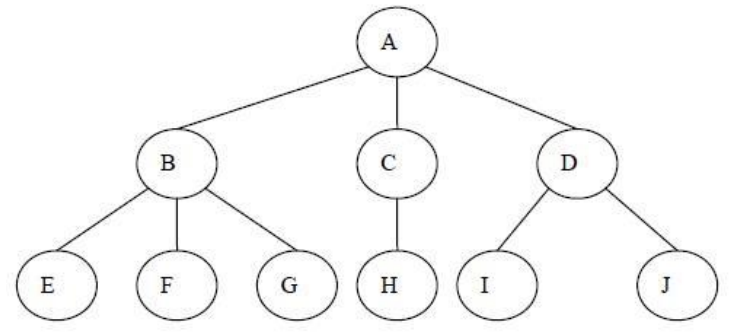
树的优点
我们之前已经学习了多种数据结构来保存数据,为什么要使用树结构来保存数据呢?
树结构和数组/链表/哈希表的对比有什么优点呢? 树的优点
数组:
优点:
- 数组的主要优点是根据下标值访问效率会很高。
- 但是如果我们希望根据元素来查找对应的位置呢?
- 比较好的方式是先对数组进行排序,再进行二分查找。
缺点:
- 需要先对数组进行排序,生成有序数组,才能提高查找效率。
- 另外数组在插入和删除数据时,需要有大量的位移操作(插入到首位或者中间位置的时候),效率很低。
链表:
优点:
- 链表的插入和删除操作效率很高。
缺点:
- 查找效率很低,需要从头开始依次访问链表中的每个数据项,直到找到。
- 而且即使插入和删除操作效率很高,但是如果要插入和删除中间位置的数据,还是需要从头先找到对应的数据。
哈希表:
优点:
- 我们学过哈希表后,已经发现了哈希表的插入、查询、删除时效率都是非常高的。
缺点:
- 空间利用率不高,底层使用的是数组,并且某些单元是没有被利用的。
- 哈希表中的元素是无序的,不能按照固定的顺序来遍历哈希表中的元素。
- 不能快速的找出哈希表中的最大值或者最小值这些特殊的值。
树结构:
- 我们不能说树结构比其他结构都要好,因为每种数据结构都有自己特定的应用场景。
- 但是树确实也综合了上面的数据结构的优点(当然优点不足于盖过其他数据结构,比如效率一般情况下没有哈希表高)。
- 并且也弥补了上面数据结构的缺点。
而且为了模拟某些场景,我们使用树结构会更加方便。
- 因为树结构是非线性的,可以表示一对多的关系。
- 比如文件的目录结构。
树的术语
在描述树的各个部分的时候有很多术语。为了让介绍的内容更容易理解,需要知道一些树的术语。不过大部分术语都与真实世界的树相关,或者和家庭关系相关(如父节点和子节点),所以它们比较容易理解。
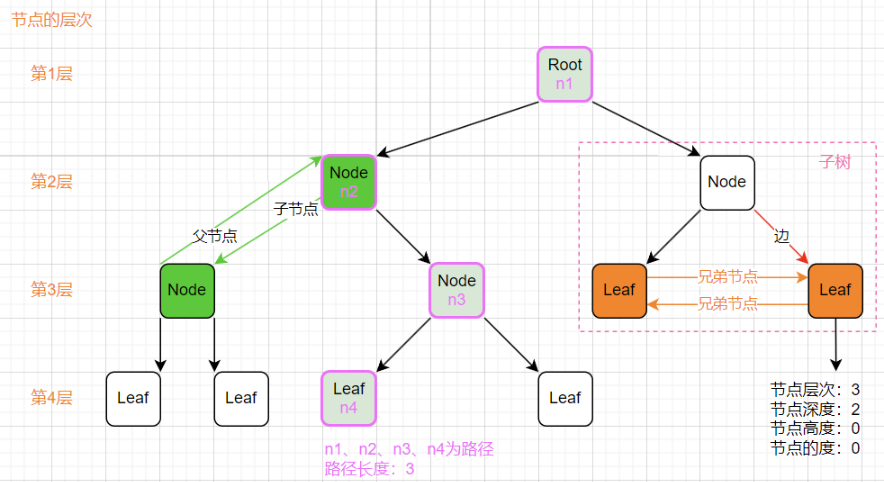
树的术语:
- 树(Tree):n(n≥0)个节点构成的有限集合。
当n=0时,称为空树;
对于任一棵非空树(n> 0),它具备以下性质:
- 树中有一个称为“根(Root)”的特殊节点,用 r 表示;
- 其余节点可分为m(m>0)个互不相交的有限集
T₁, T₂, ..., Tₘ,其中每个集合本身又是一棵树,称为原来树的“子树(SubTree)”
- 根节点(root node):位于二叉树顶层的节点,没有父节点。
- 叶节点(leaf node):没有子节点(度为0)的节点,其两个指针均指向
None。 - 子节点(Child):若A节点是B节点的父节点,则称B节点是A节点的子节点;子节点也称孩子节点。
- 父节点(Parent):有子树的节点是其子树的根节点的父节点。
- 兄弟节点(Sibling):具有同一父节点的各节点彼此是兄弟节点。
- 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。
- 树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 边(edge):连接两个节点的线段,即节点引用(指针)。
- 路径:从节点n₁到nₖ的路径为一个节点序列
n₁,n₂,… ,nₖ。nᵢ是 nᵢ₊₁的父节点。 - 路径长度:路径所包含边的个数为路径的长度。
树的表示方式
普通表示方式:
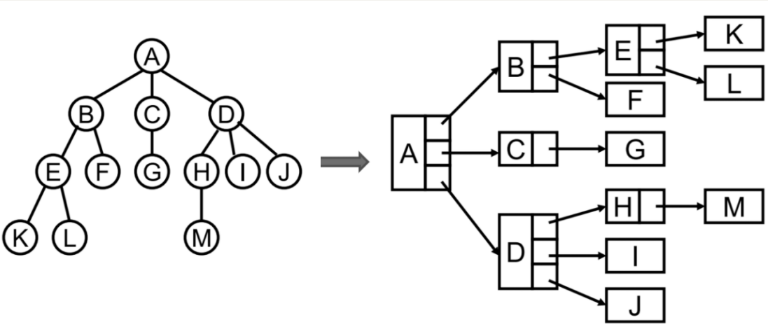
const ANode = { value: 'A', leftNode: BNode, centerNode: CNode, rightNode: DNode }儿子-兄弟表示法:
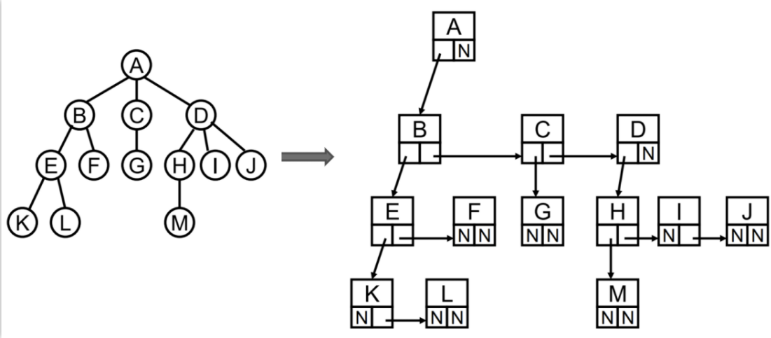
const ANode = { value: 'A', sunNode: BNode, siblingNode: null }
const BNode = { value: 'B', sunNode: ENode, siblingNode: CNode }
const CNode = { value: 'C', sunNode: GNode, siblingNode: DNode }
const DNode = { value: 'D', sunNode: HNode, siblingNode: null }儿子-兄弟表示法旋转:
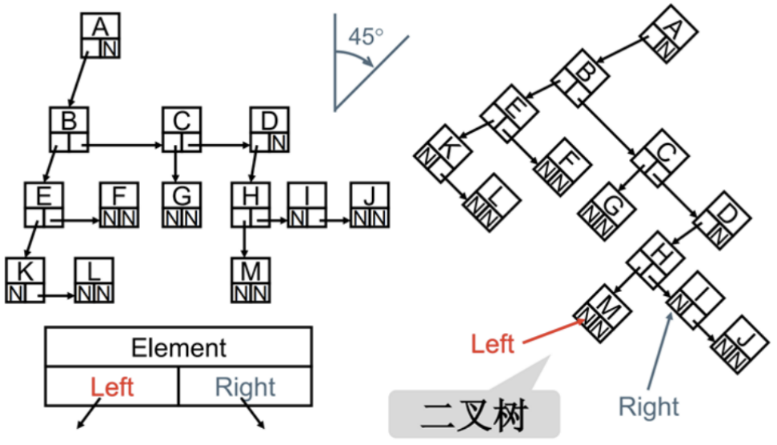
const ANode = { value: 'A', sunNode: BNode, siblingNode: null }
const BNode = { value: 'B', sunNode: ENode, siblingNode: CNode }
const CNode = { value: 'C', sunNode: GNode, siblingNode: DNode }你发现上面规律了吗?
- 其实所有的树本质上都可以使用二叉树模拟出来。
- 所以在学习树的过程中,二叉树非常重要。
二叉树
概述
概念
如果树中每个节点最多只能有两个子节点,这样的树就成为"二叉树"。
前面我们已经提过二叉树的重要性,不仅仅是因为简单,也因为几乎上所有的树都可以表示成二叉树的形式。
二叉树的定义:
- 二叉树可以为空,也就是没有节点。
- 若不为空,则它是由根节点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。
二叉树有五种形态:
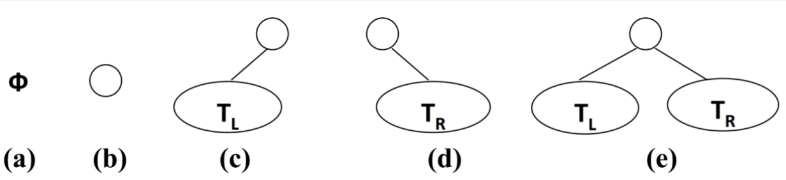
二叉树的特性
二叉树有几个比较重要的特性,在笔试题中比较常见:
- 一颗二叉树第i层的最大节点数为:
2ⁱ⁻¹,i >= 1; - 深度为k的二叉树有最大节点总数为:
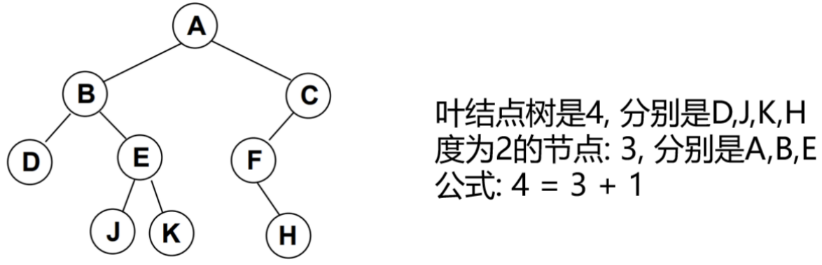
2ᵏ-1,k >= 1; - 对任何非空二叉树T,若n₀表示叶节点的个数、n₂是度为2的非叶节点个数,那么两者满足关系
n₀ = n₂ + 1。
二叉树的分类
- 完美二叉树:每个节点都有左右两个子节点,且所有叶子节点都在同一层。
- 完全二叉树:除了最后一层外,其他层的节点都满;最后一层的节点集中在左侧。
- 平衡二叉树:左右子树的高度差不超过1。
- 二叉搜索树(BST):对于树中的每个节点,左子树的值小于该节点,右子树的值大于该节点。
完美二叉树
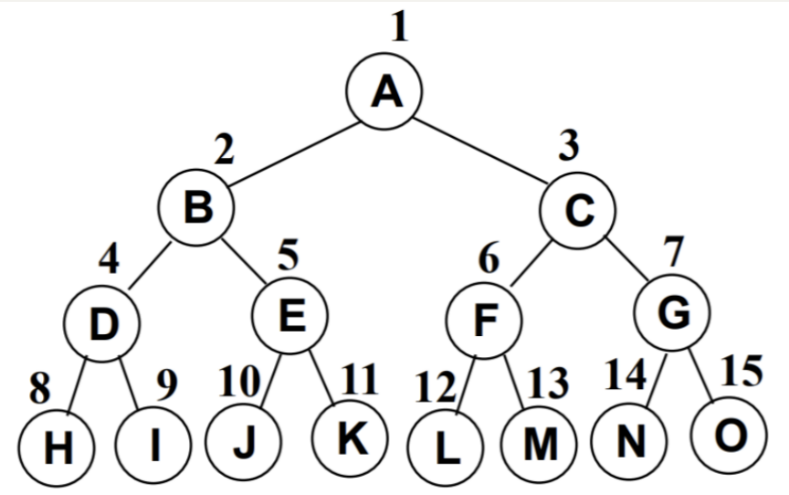
完美二叉树(Perfect Binary Tree,Full Binary Tree,满二叉树):在二叉树中,除了最下一层的叶节点外,每层节点都有2个子节点,就构成了满二叉树。
完全二叉树
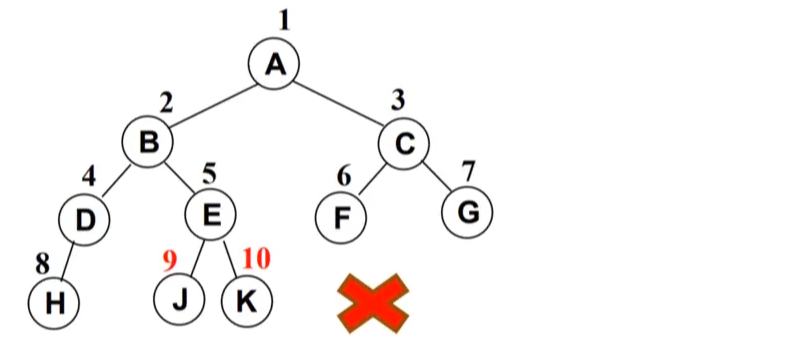
完全二叉树(Complete Binary Tree):除二叉树最后一层外,其他各层的节点数都达到最大个数。且最后一层从左向右的叶节点连续存在,只缺右侧若干节点。完美二叉树是特殊的完全二叉树。
下面不是完全二叉树,因为D节点还没有右节点,但是E节点就有了左右节点。
二叉树存储
二叉树的存储常见的方式是数组和链表。
数组存储
完全二叉树:按从上至下、从左到右顺序存储
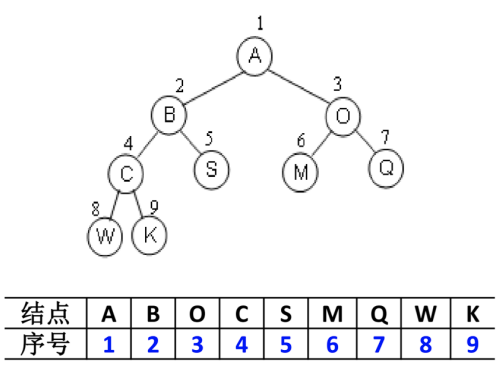
非完全二叉树:非完全二叉树要补全成完全二叉树才可以按照上面的方案存储。但是会造成很大的空间浪费。
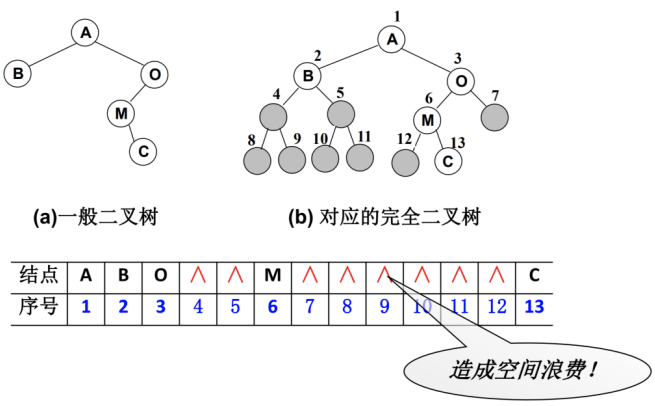
链表存储
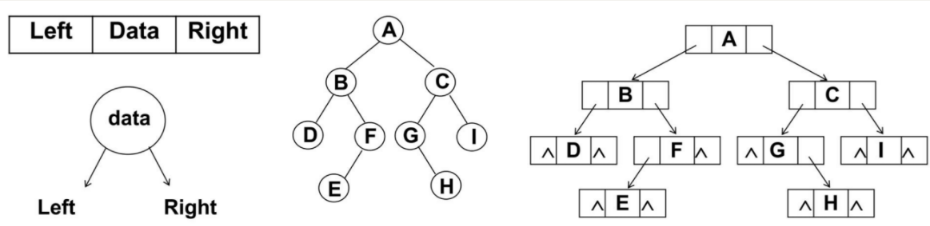
二叉树最常见的方式还是使用链表存储。
思路:每个节点封装成一个Node,Node中包含存储的数据,左节点的引用,右节点的引用。
二叉搜索树
概述
概念
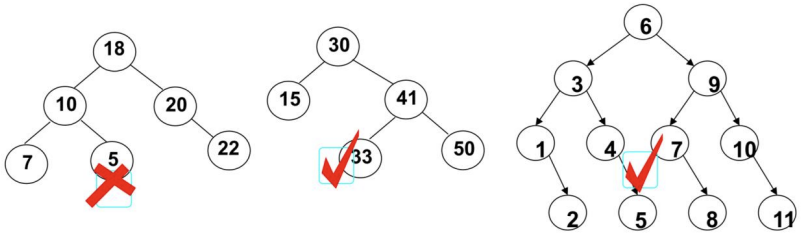
二叉搜索树(BST,Binary Search Tree,二叉排序树,二叉查找树):满足以下条件:
- 1、对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 2、任意节点的左、右子树也是二叉搜索树,即同样满足条件1。
二叉搜索树的上述性质使得它的查找效率非常高。
查找、插入
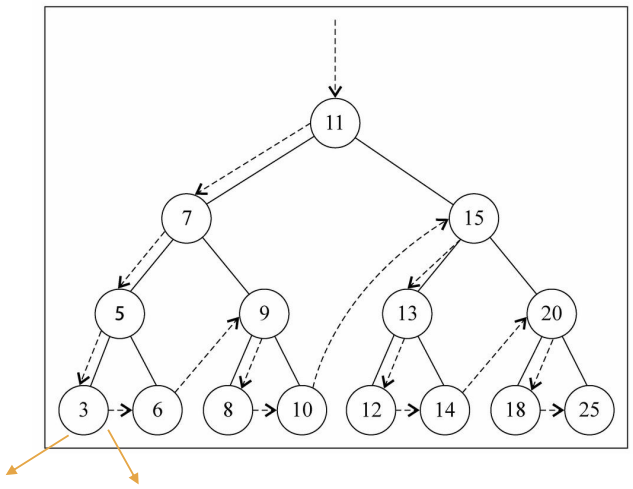
示例:在二叉搜索树中查找值为10的节点
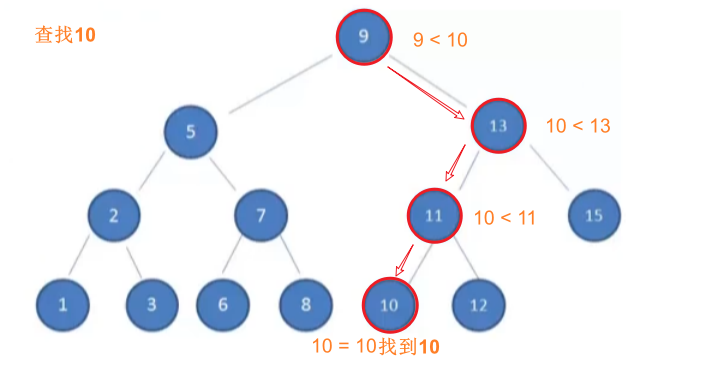
上述方式就是二分查找的思想
- 查找所需的最大次数等于二叉搜索树的深度;
- 插入节点时,也利用类似的方法,一层层比较大小,找到新节点合适的位置。
二叉搜索树实现
API
二叉搜索树的常见操作:
插入操作:
- insert():
(value),向树中插入一个新的数据。
遍历操作:
inOrderTraverse():
(),通过中序遍历方式遍历所有节点。preOrderTraverse():
(),通过先序遍历方式遍历所有节点。postOrderTraverse():
(),通过后序遍历方式遍历所有节点。levelOrderTraverse():
(),通过层序遍历方式遍历所有节点。
查找操作:
getMinValue():
(),返回树中最小的值。getMaxValue():
(),返回树中最大的值。search():
(value),在树中查找一个数据,如果节点存在,则返回true;如果不存在,则返回false。
删除操作:
- remove():
(value),从树中移除某个数据。
BSTree 类
我们像封装其他数据结构一样,先来封装一个BSTree的类
图解:
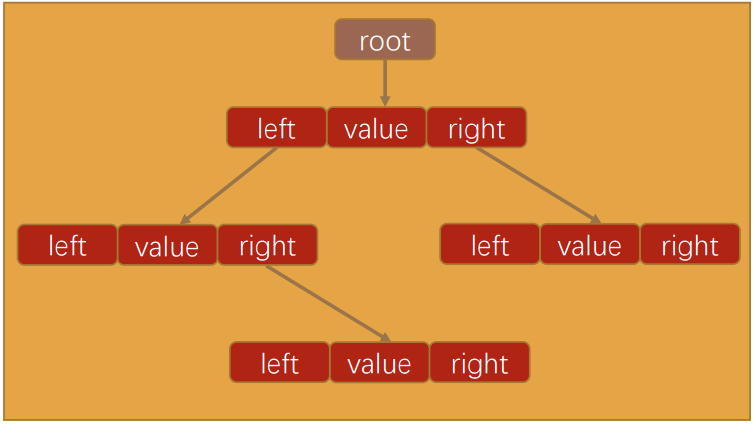
代码解析:
- 封装BSTree类:
- 对于BSTree来说,只需要保存根节点即可,因为其他节点都可以通过根节点找到。
- 封装Node类:还需要封装一个用于保存每一个节点的Node类。
- 该类包含三个属性:节点对应的value,指向的左子树left,指向的右子树right。
代码实现:
1、封装Node类
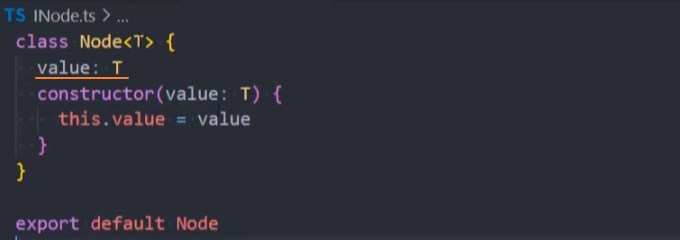
2、封装TreeNode类,它继承Node类
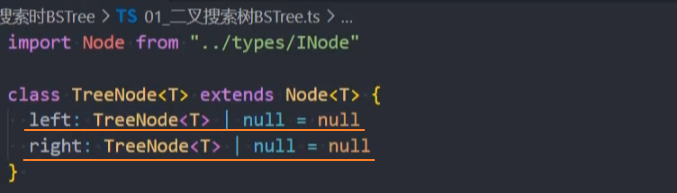
3、封装BSTree类

insert() 插入
insert():(value),向树中插入一个新的数据。
图解:
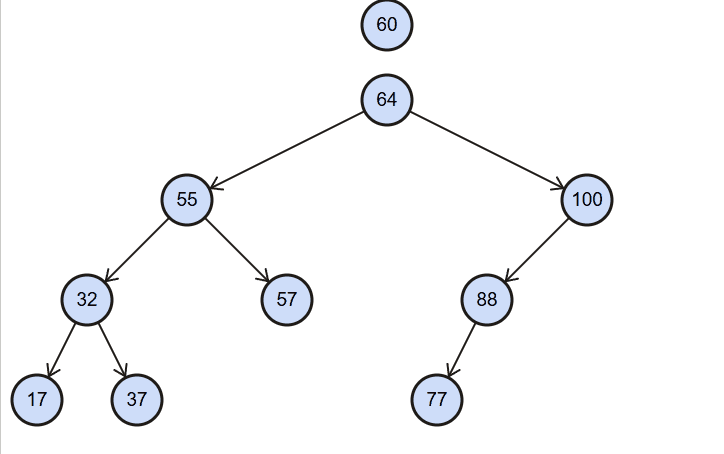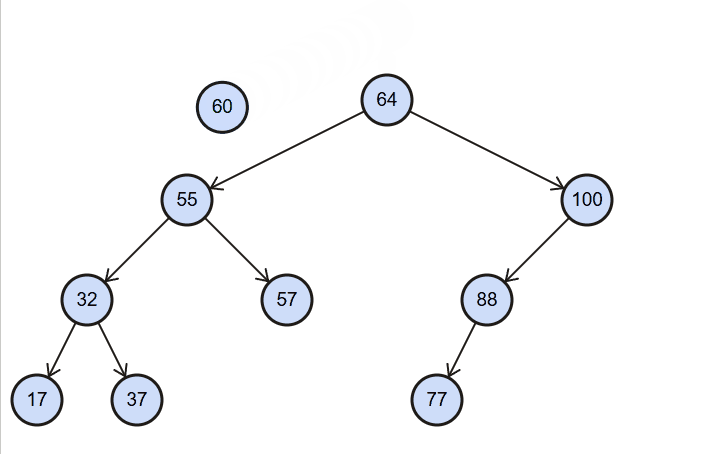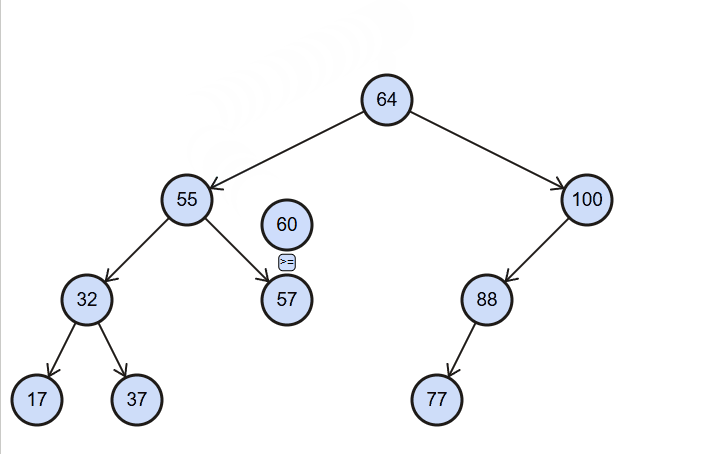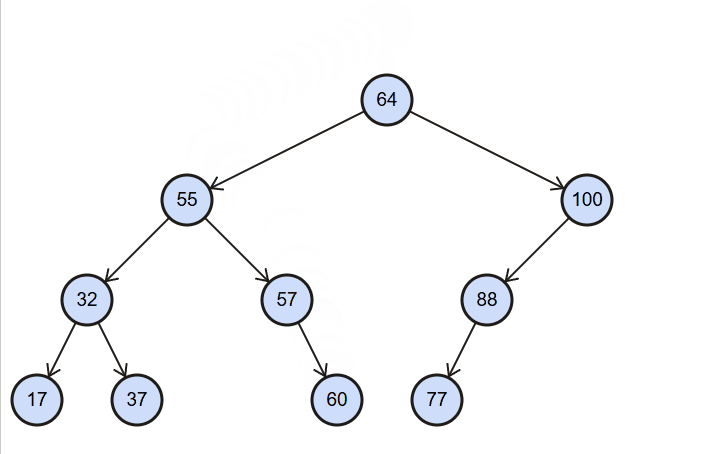
代码实现:
1、封装insert()方法
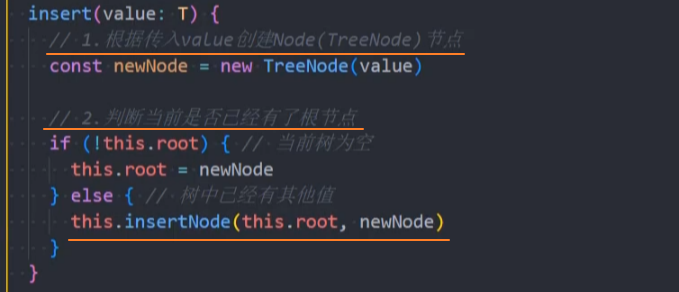
2、封装insertNode()方法
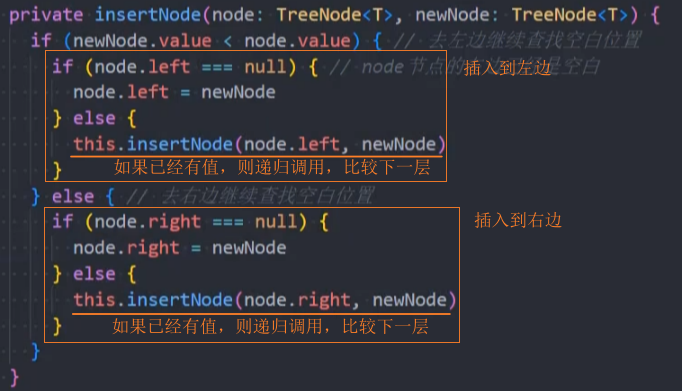
3、测试:调用insert()方法。同时安装 hy-algokit 插件,打印生成的树结构
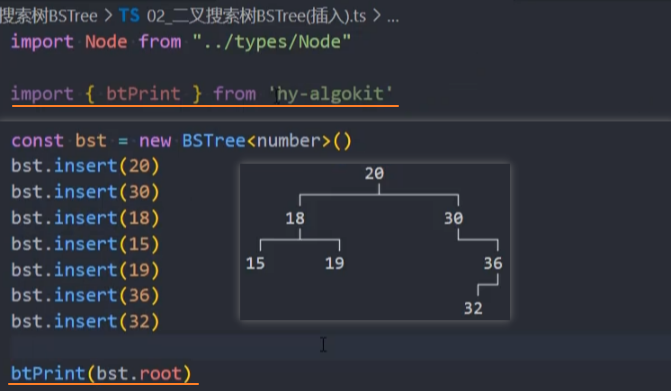
▸ 优化:在类的内部封装打印方法print()
上述的方法中需要在类的外部访问root,不太安全。

遍历二叉搜索树
前面,我们向树中插入了很多的数据,为了能看到测试结果。我们先来学习一下树的遍历。
这里我们学习的树的遍历,针对所有的二叉树都是适用的,不仅仅是二叉搜索树。
树的遍历:
- 遍历一棵树是指访问树的每个节点(也可以对每个节点进行某些操作,我们这里就是简单的打印)
- 但是树和线性结构不太一样,线性结构我们通常按照从前到后的顺序遍历,但是树呢?
- 应该从树的顶端还是底端开始呢? 从左开始还是从右开始呢?
二叉树常见的遍历方式有四种:
- 先序遍历
- 中序遍历
- 后序遍历
- 层序遍历
preOrderTraverse() 先序遍历
preOrderTraverse():(),通过先序遍历方式遍历所有节点。
思路图解:
- 1、访问根节点
- 2、先序遍历其左子树
- 3、先序遍历其右子树
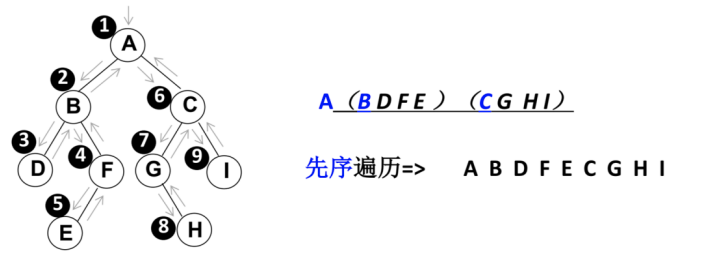
代码实现:递归法
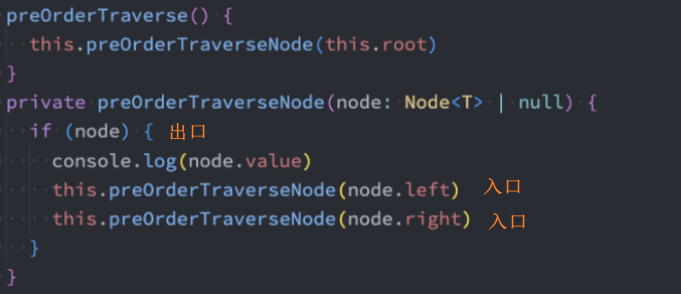
代码实现:非递归法
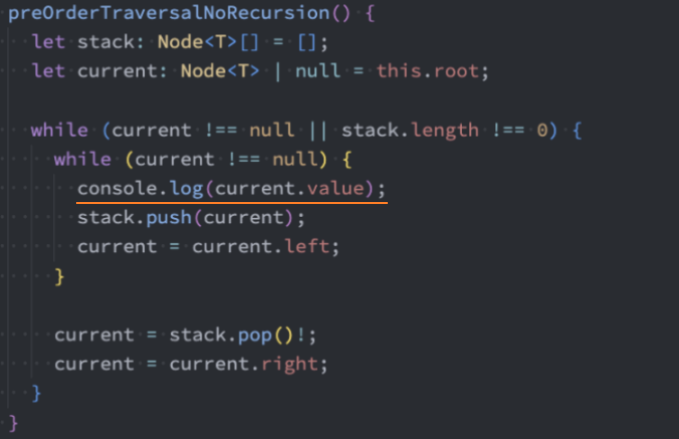
inOrderTraverse() 中序遍历
inOrderTraverse():(),通过中序遍历方式遍历所有节点。
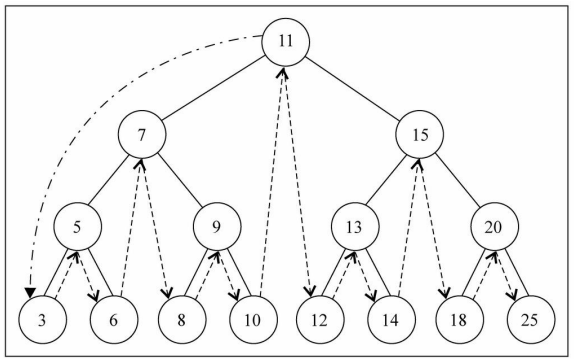
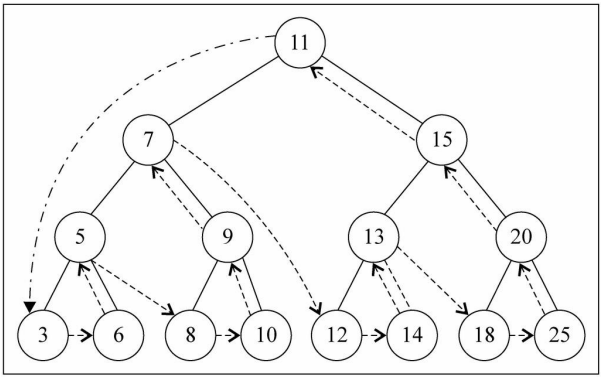
遍历过程为:
- ①中序遍历其左子树;
- ②访问根节点;
- ③中序遍历其右子树。
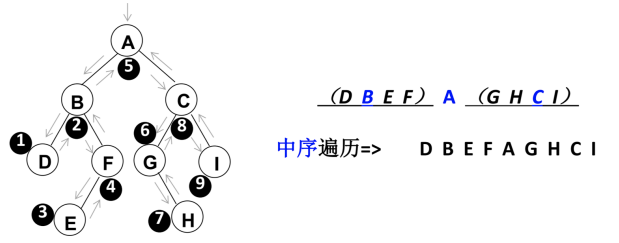
代码实现:递归法
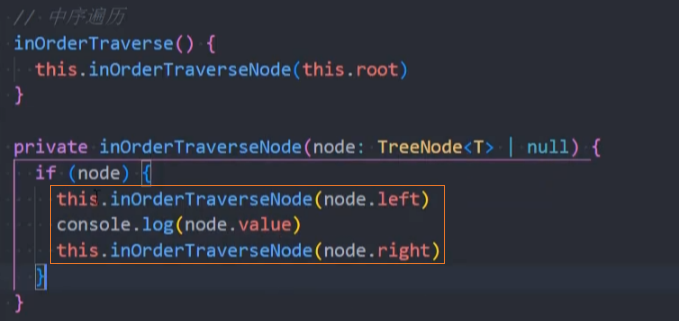
代码实现:非递归法
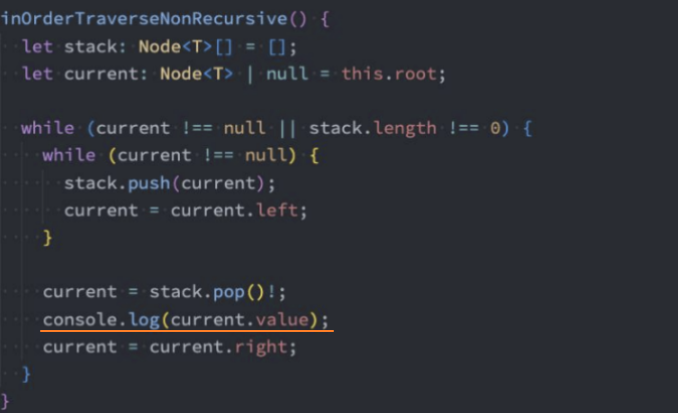
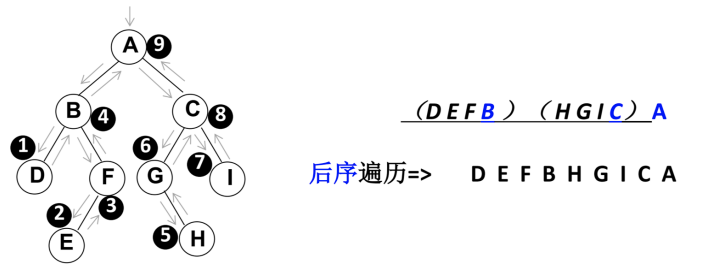
postOrderTraverse() 后序遍历
postOrderTraverse():(),通过后序遍历方式遍历所有节点。
遍历过程为:
- ①后序遍历其左子树;
- ②后序遍历其右子树;
- ③访问根节点。
代码实现:递归法
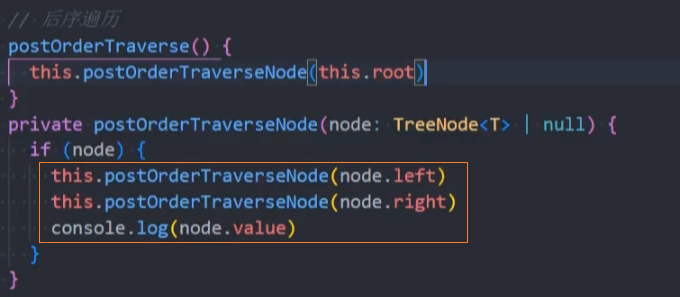
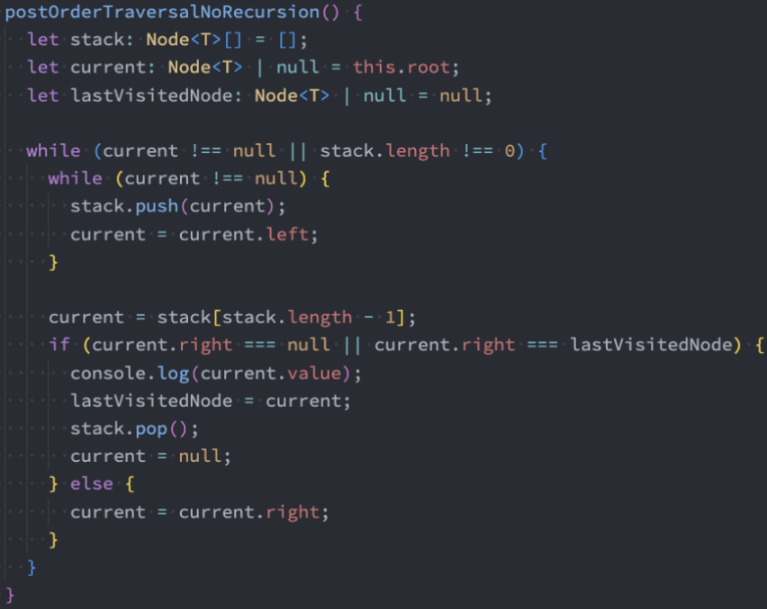
代码实现:非递归法
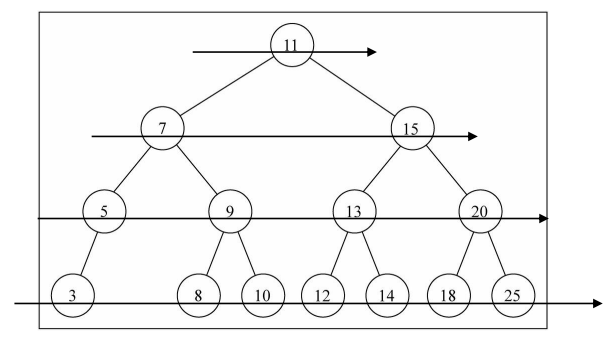
levelOrderTraverse() 层序遍历
levelOrderTraverse():(),通过层序遍历方式遍历所有节点。
遍历思路: 层序遍历很好理解,就是从上向下逐层遍历。层序遍历通常我们会借助队列来完成,也是队列的一个经典应用场景;
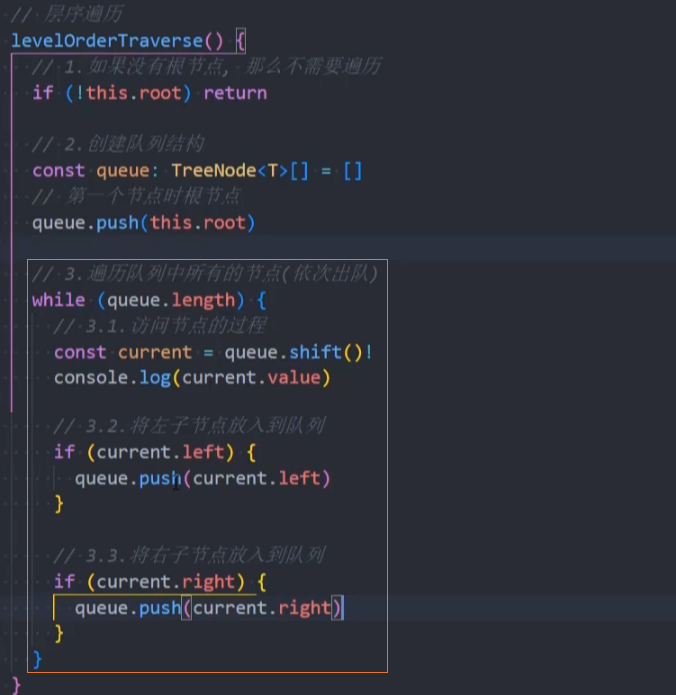
代码实现:非递归法
获取最值
getMinValue() 最小值
getMinValue():(),返回树中最小的值。
在二叉搜索树中搜索最值是一件非常简单的事情,其实用眼睛看就可以看出来了。
图解:
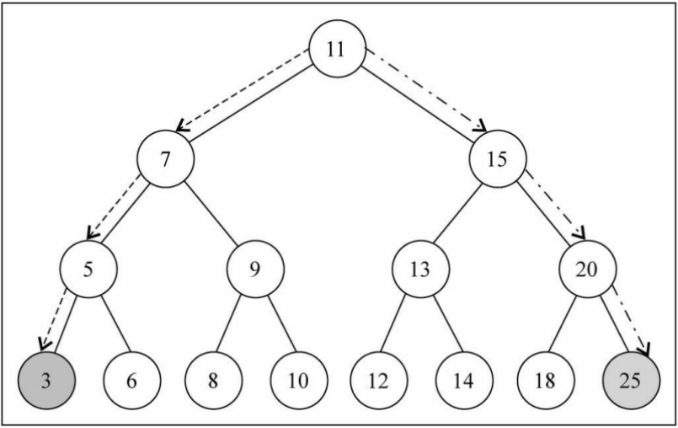
代码实现:
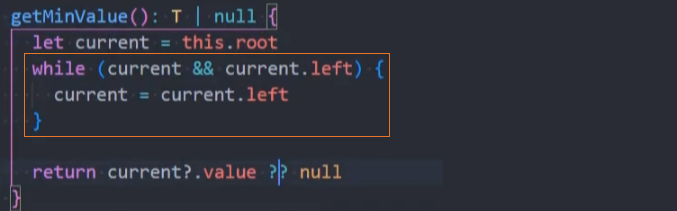
getMaxValue() 最大值
getMaxValue():(),返回树中最大的值。
代码实现:
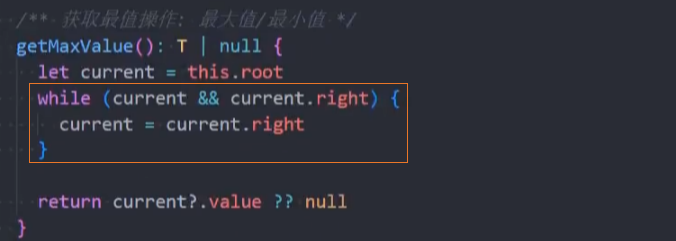
search() 搜索
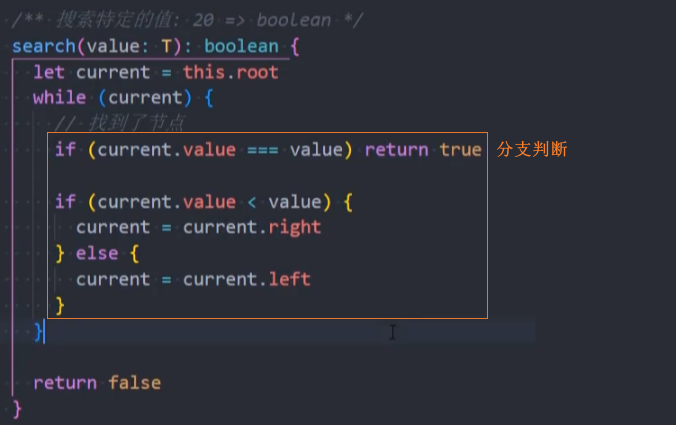
search():(value),在树中查找一个数据,如果节点存在,则返回true;如果不存在,则返回false。
二叉搜索树不仅仅获取最值效率非常高,搜索特定的值效率也非常高。
代码实现:递归法
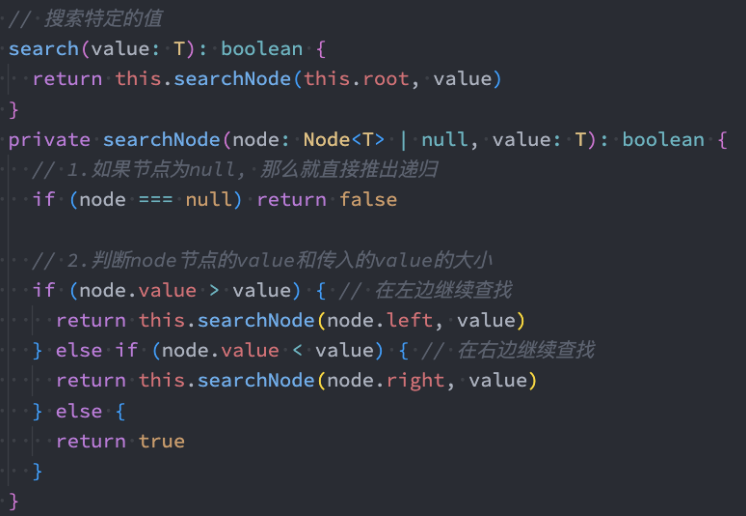
代码实现:非递归法
remove() 删除@
remove():(value),从树中移除某个数据。
思路图解:
二叉搜索树的删除有些复杂,我们一点点完成。
1、查找要删除的节点。如果节点不存在则不需要删除。
2、找到后考虑三种情况:
- 情况一:该节点没有子节点(简单)
- 情况二:该节点有一个子节点(简单)
- 情况三:该节点有二个子节点(复杂)
3、情况一:该节点没有子节点(简单)
如果只有一个单独的根,直接删除该根

如果是叶节点,将该节点的父节点的left或right设为null
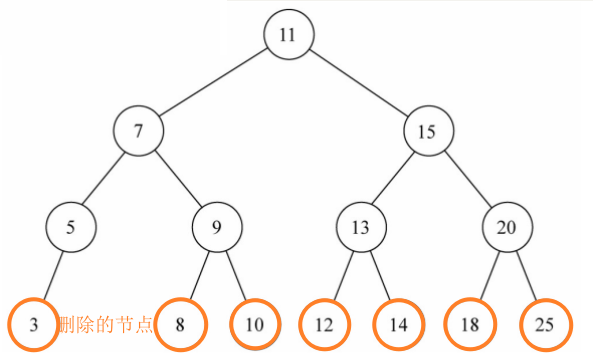
4、情况二:该节点有一个子节点(简单)
如果删除的是根节点,直接将其子节点赋值给root
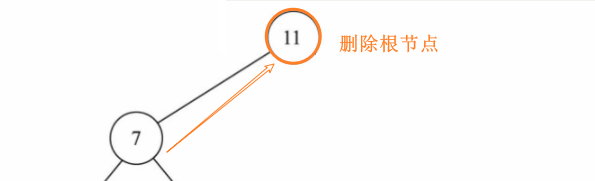
修改该节点的父节点直接指向其子节点
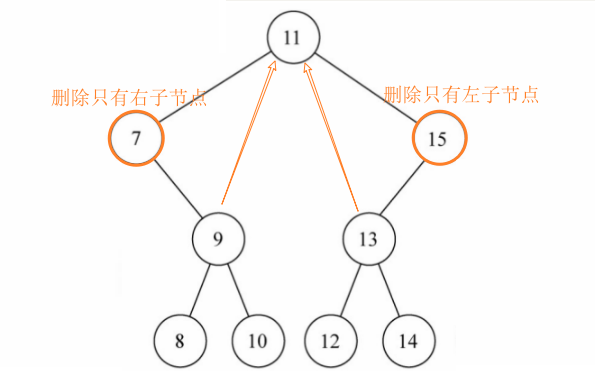
5、情况三:该节点有二个子节点(复杂)
情况1:删除9节点,用9节点的某个后代(8或10)替代9的位置
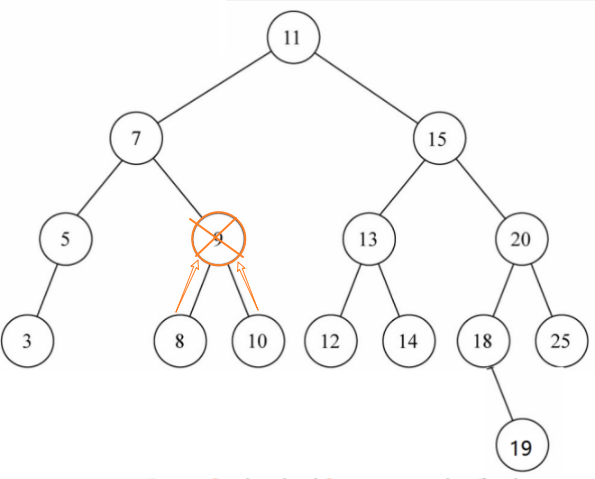
情况2:删除7节点,用7节点的某个后代(5或8)替代7的位置,注意: 不是5或9
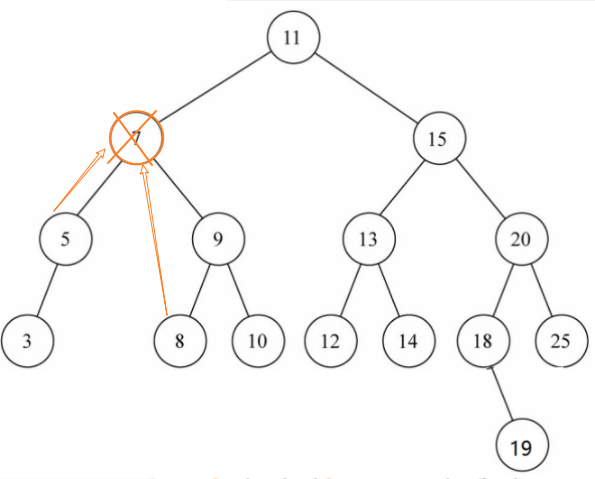
情况3:删除15节点,用15的某个后代(14或18)替代15的位置
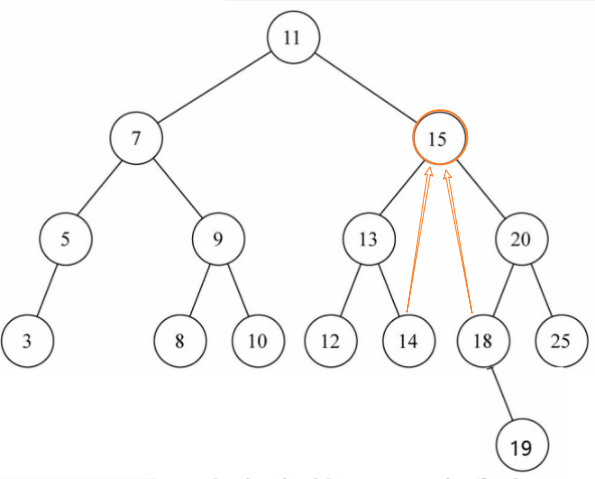
规律:被删除节点的后代替代节点,可以是:
- 去左边找一个比删除节点小一些的节点,但是是左子树的最大节点,该点称为 前驱节点。
- 去右边找一个比删除节点大一些的节点,但是是右子树的最小节点,该点称为 后继节点。
搜索节点和父节点
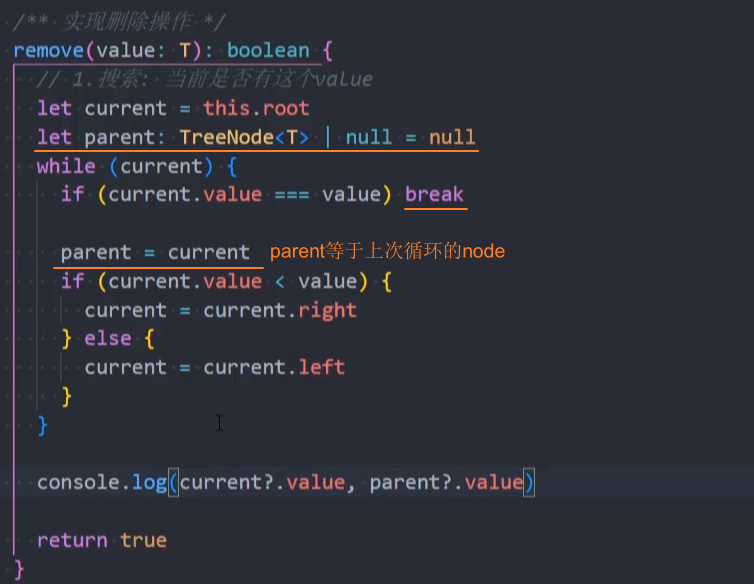
重构:搜索节点
remove()和之前的search()方法的代码结构类似,可以合并
1、在search()方法中调用私有方法searchNode()

2、在remove()方法中调用私有方法searchNode()
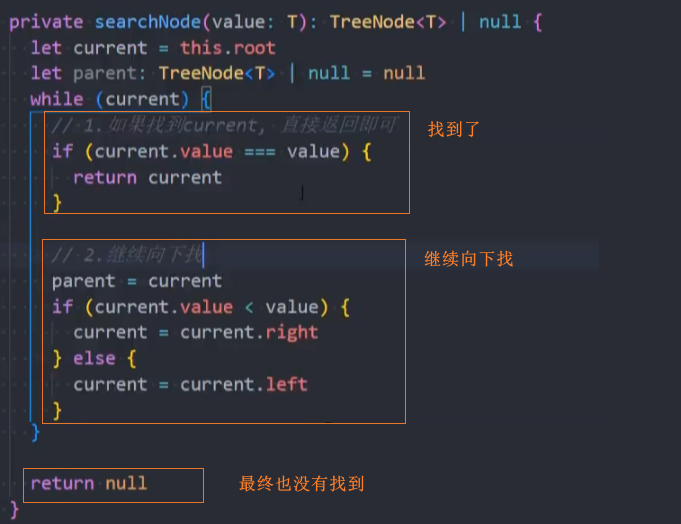
3、实现抽取的搜索方法searchNode()
4、优化: 同时获取parent节点
为TreeNode节点添加
parent属性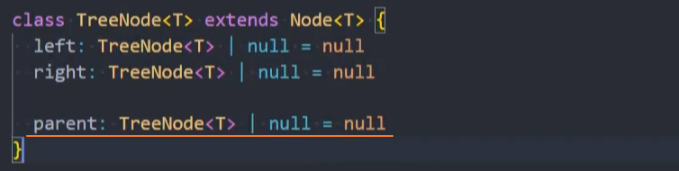
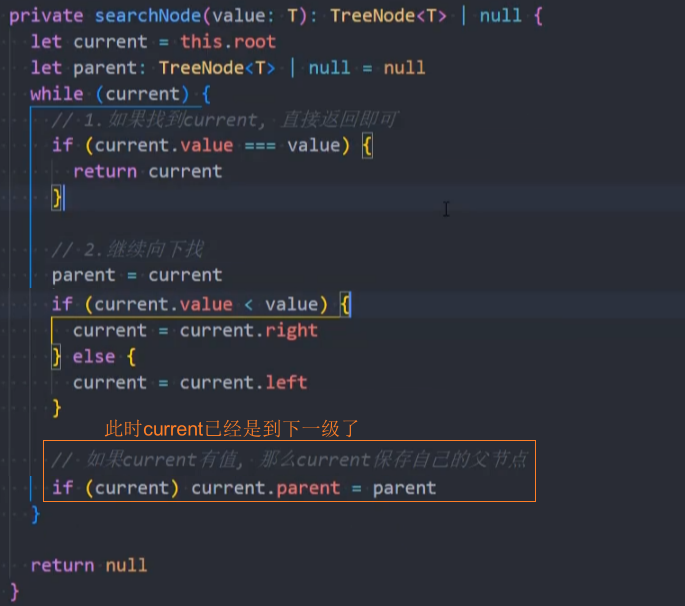
在searchNode()方法中为parent赋值
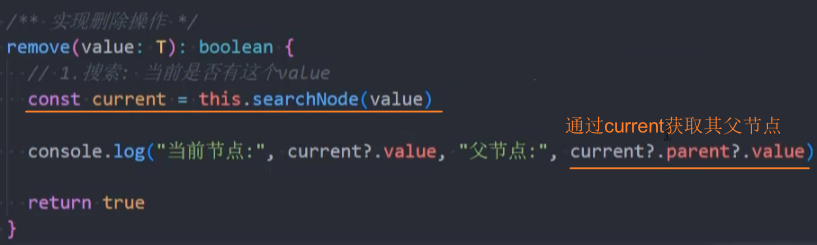
在remove()方法中可以通过current获取其父节点
5、优化: 判断当前节点在其父节点的左边还是右边
为TreeNode节点添加
get isLeft()和get isRight()方法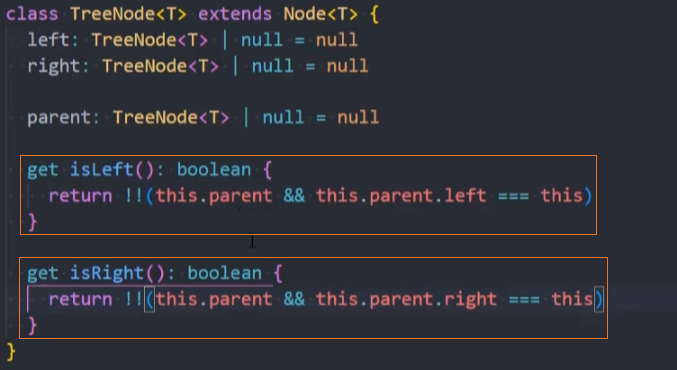
在remove()方法中调用判断当前节点在其父节点的左边还是右边
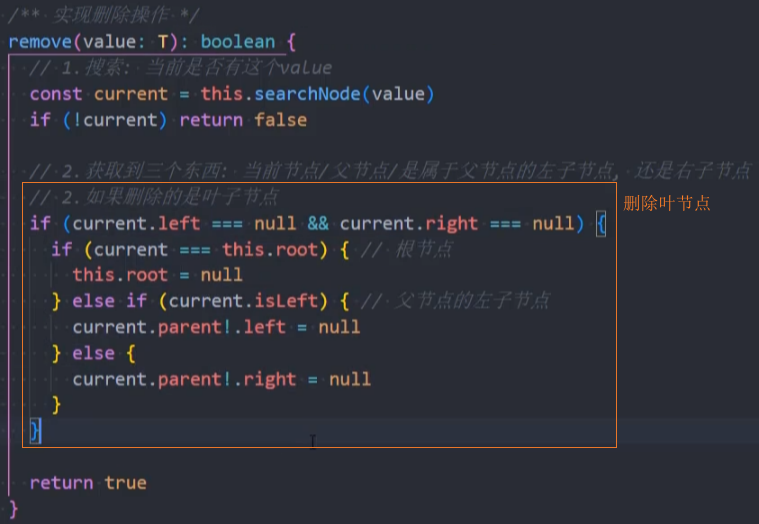
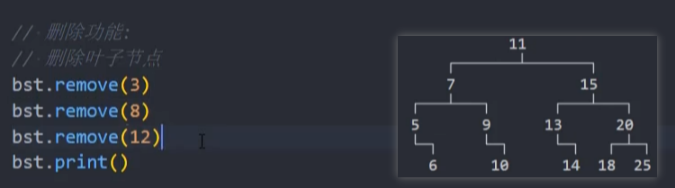
情况一:叶节点
如果只有一个单独的根,直接删除该根

如果是叶节点,将该节点的父节点的left或right设为null

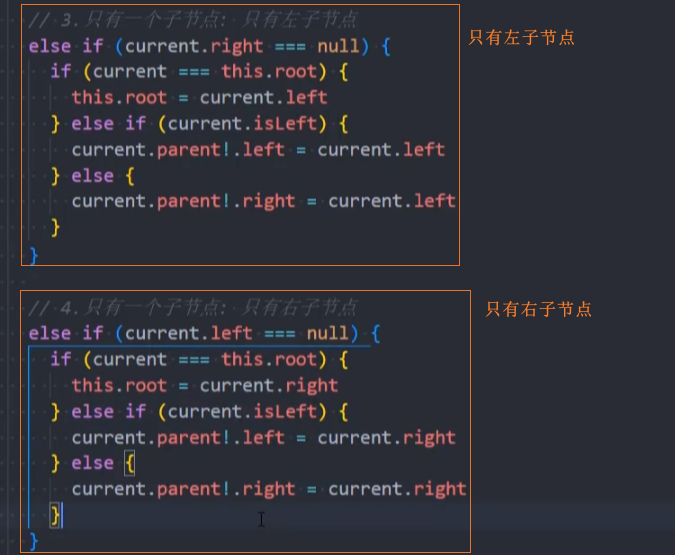
情况二:一个子节点
如果删除的是根节点,直接将其子节点赋值给root

修改该节点的父节点直接指向其子节点

情况三:两个子节点
情况1:删除9节点,用9节点的某个后代(8或10)替代9的位置

情况2:删除7节点,用7节点的某个后代(5或8)替代7的位置,注意: 不是5或9

情况3:删除15节点,用15的某个后代(14或18)替代15的位置

规律:被删除节点的后代替代节点,可以是:
- 去左边找一个比删除节点小一些的节点,但是是左子树的最大节点,该点称为 前驱节点。
- 去右边找一个比删除节点大一些的节点,但是是右子树的最小节点,该点称为 后继节点。
1、实现获取后继节点的方法getSuccessor()
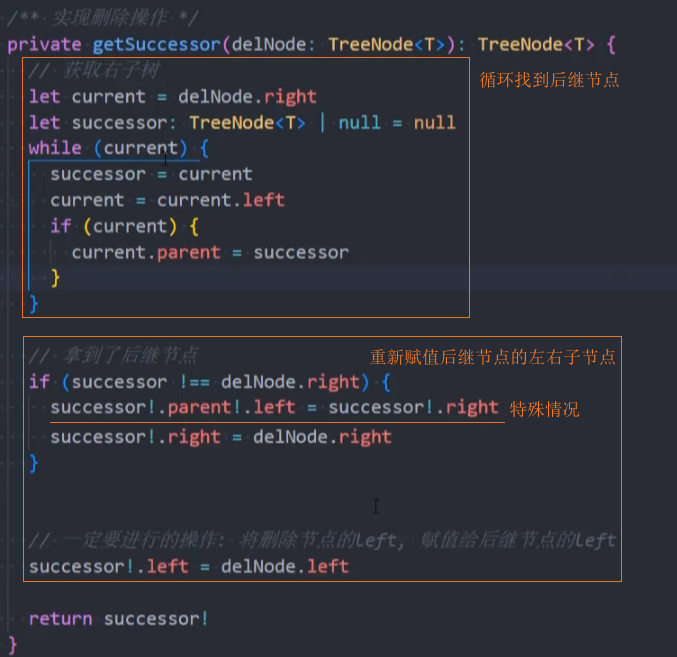
2、用后继节点替换被删除的节点
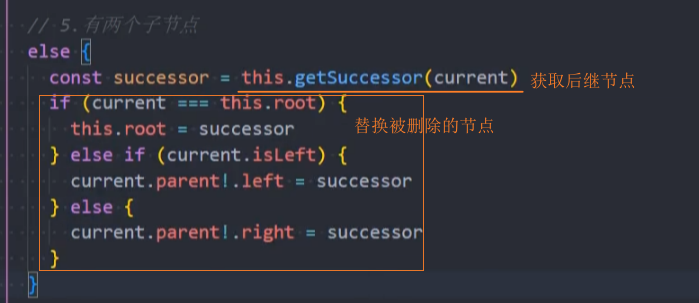
重构:删除节点
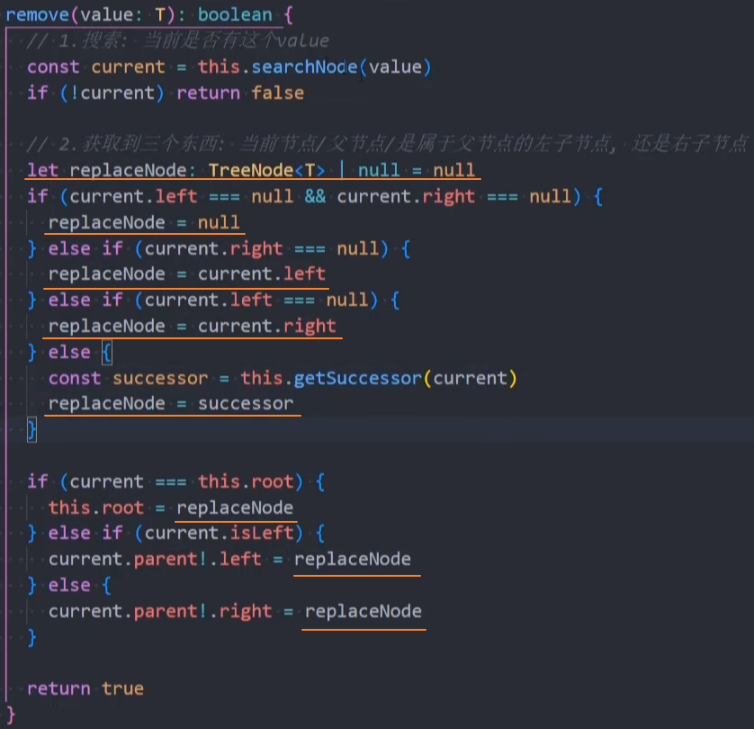
插入对象@
我们不但可以在二叉搜索树中存放对象数字,还可以存放对象等类型的数据。
1、创建一个Product产品类

2、通过Product创建对象实例,并插入到bst树中
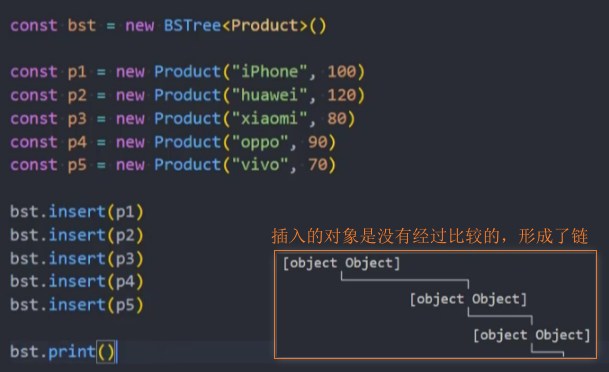
3、问题:此时插入的对象是没有经过比较的,形成了链结构。
解决思路:可以通过在Product类中,重写valueOf()方法,让对象可以比较price属性。
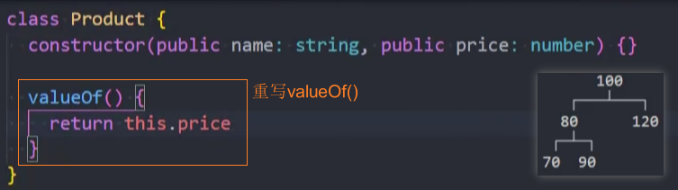
4、优化:打印树时,显示更多信息。
思路:
- 导入 hy-algokit 包中的接口 PrintableNode 并implements实现它,以此约束Node类的属性。
- 在自定义的
get value()方法中,返回想要打印的信息。
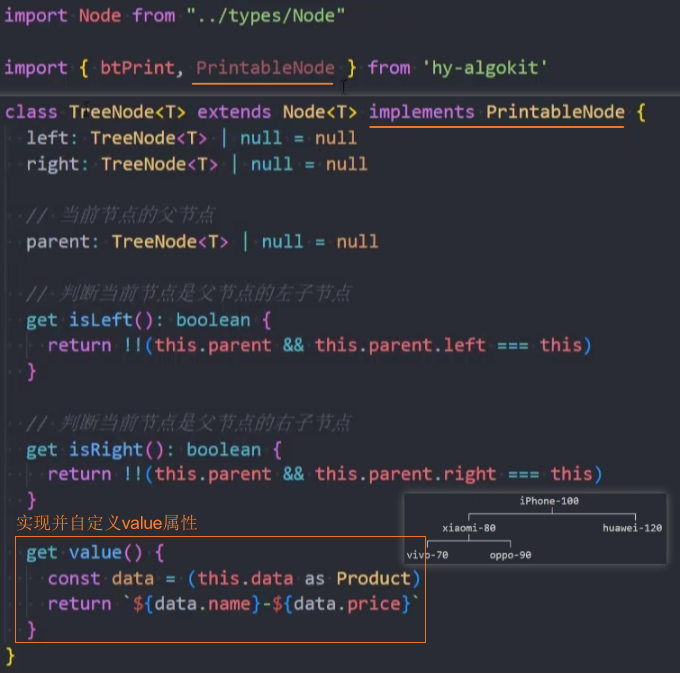
总结
看到这里,你就会发现删除节点相当棘手。
实际上,因为它非常复杂,一些程序员都尝试着避开删除操作,因此就出现了其他删除节点的思路:
思路一:
- 1、在Node类中添加一个isDeleted字段。
- 2、删除某节点时,就设置
isDeleted = true。 - 3、在查找操作时,先判断节点的isDeleted值。
- 优点:实现起来比较简单,每次删除节点不会改变原有的树结构。
- 缺点:在存储中依然保留着被删除的节点。
思路二:
- 1、只修改被删除节点的value值为后继节点的值:
delNode.value = successor.value - 2、后继节点后的节点结构依然调整。
二叉搜索树的缺陷
优势:二叉搜索树作为数据存储的结构有重要的优势:
可以快速地找到给定关键字的数据项 并且可以快速地插入和删除数据项。
问题: 二叉搜索树有一个很麻烦的问题:插入有序数据 会形成 非平衡树。
如果插入的数据是有序的数据,比如下面的情况:有一棵初始化为 9 8 12 的二叉树,插入下面的数据:7 6 5 4 3
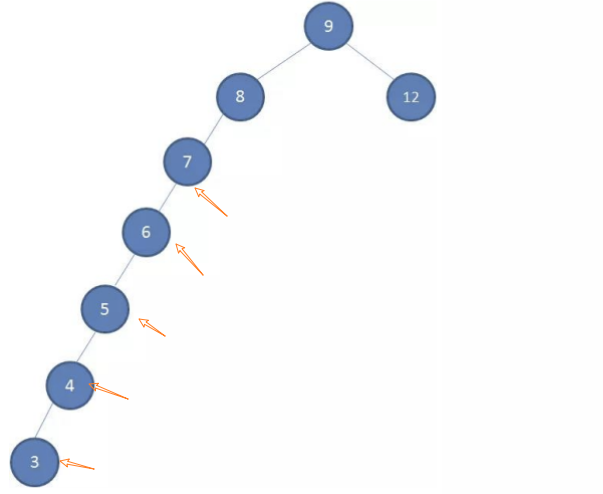
非平衡树(Unbalanced Tree) 指在树的数据结构中,节点的左右子树的高度差异较大,导致树形结构不平衡,可能会影响其性能表现,特别是在查找、插入和删除操作时。查找效率由O(logN)变成了O(N)。
平衡树
为了能以较快的时间O(logN)来操作一棵树,我们需要保证树总是平衡的:
- 至少大部分是平衡的,那么时间复杂度也是接近O(logN)的
- 也就是说树中每个节点左边的子孙节点的个数,应该尽可能的等于右边的子孙节点的个数。
常见的平衡树:
AVL树:是最早的一种平衡树,它通过在每个节点多存储一个额外的数据保持树的平衡。时间复杂度为O(logN)。
红黑树:也通过一些特性来保持树的平衡。时间复杂度为O(logN)。
对比: 插入/删除等操作,红黑树性能优于AVL树。红黑树因此应用更多。
平衡二叉树
平衡树 Balanced Tree
平衡树(Balanced Tree) 是一种特殊的二叉搜索树,其目的是通过一些特殊的技巧来维护树的高度平衡。从而保证树的搜索、插入、删除等操作的时间复杂度都较低。
为什么需要平衡树:
一棵树如果退化成链状结构,那么搜索、插入、删除等操作的时间复杂度就会达到最坏情况,即O(n)。
平衡树通过不断调整树的结构,使得树的高度尽量平衡,从而保证搜索、插入、删除等操作的时间复杂度都较低,通常为O(logn)。因此,如果我们需要高效地处理大量的数据,那么平衡树就显得非常重要了。
应用: 平衡树的应用非常广泛,如索引、内存管理、图形学等领域均有广泛使用。
插入有序数字导致树不平衡:
比如我们连续的插入1、2、3、4、5、6的数字,那么前面的二叉搜索树最终形成的结构如下
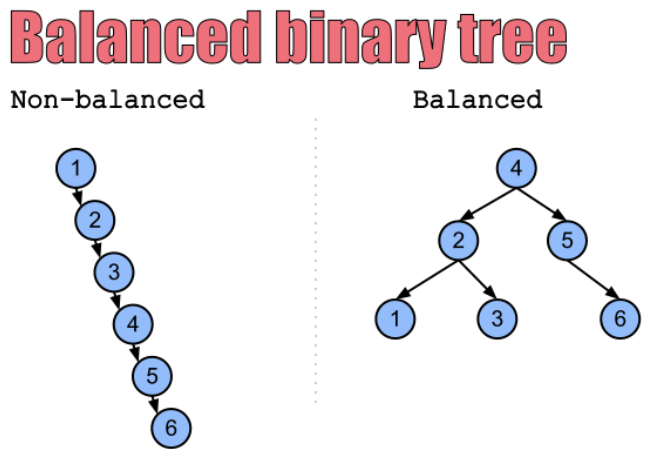
删除元素导致树不平衡:
事实上不只是添加会导致树的不平衡,删除元素也可能会导致树的不平衡。
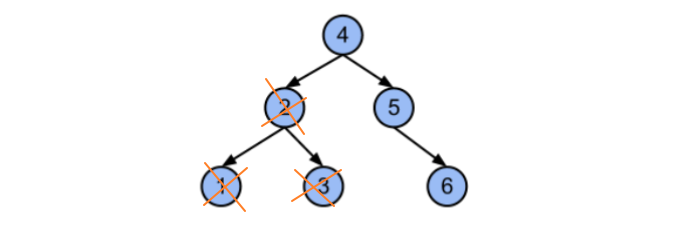
平衡树的方式
方式一:限制插入、删除节点。在树特性的状态下,不允许插入或者删除某些节点,不现实。
方式二:使用特定方式再平衡树。在随机插入或者删除元素后,通过某种方式观察树是否平衡,如果不平衡通过特定的方式(比如旋转),让树保持平衡。
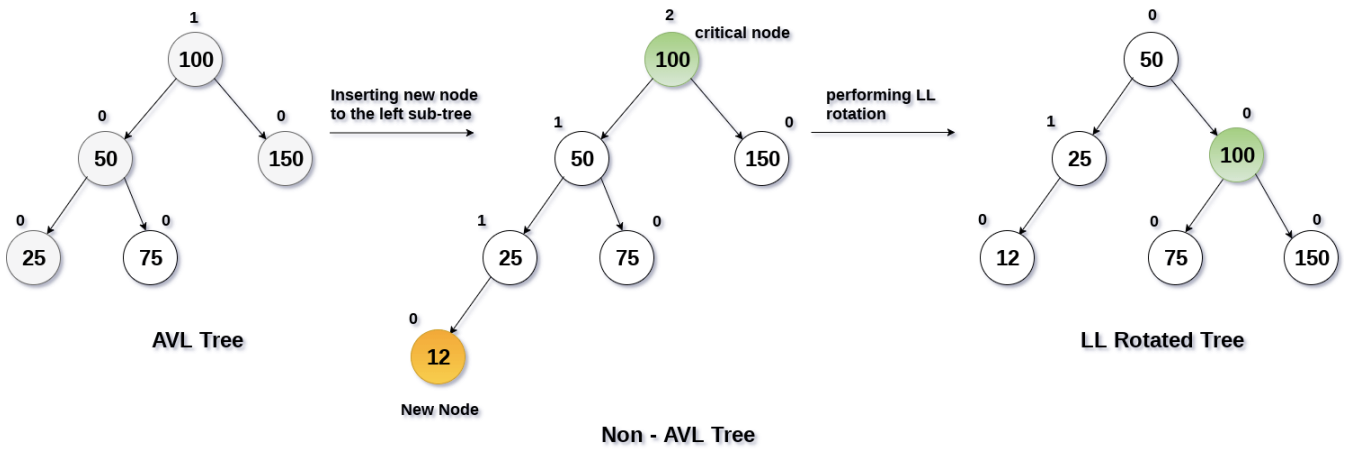
常见的平衡二叉搜索树
常见的平衡二叉搜索树有哪些呢?
- AVL树:这是一种最早的平衡二叉搜索树,在1962年由G.M. Adelson-Velsky和E.M. Landis发明。
- 红黑树:这是一种比较流行的平衡二叉搜索树,由R. Bayer在1972年发明。
- Splay树:这是一种动态平衡二叉搜索树,通过旋转操作对树进行平衡。
- Treap:这是一种随机化的平衡二叉搜索树,是二叉搜索树和堆的结合。
- B-树:这是一种适用于磁盘或其他外存存储设备的多路平衡查找树。
这些平衡二叉搜索树都用于保证搜索树的平衡,从而在插入、删除、查找操作时保证了较低的时间复杂度。
红黑树和AVL树是应用最广泛的平衡二叉搜索树:
- 红黑树:红黑树被广泛应用于实现诸如操作系统内核、数据库、编译器等软件中的数据结构,其原因在于它在插入、删除、查找操作时都具有较低的时间复杂度。
- AVL树:AVL树被用于实现各种需要高效查询的数据结构,如计算机图形学、数学计算和计算机科学研究中的一些特定算法。
AVL树
概述
AVL树(Adelson-Velsky and Landis Tree) 是一种自平衡的二叉搜索树,其特点是通过维护每个节点的平衡因子来保持树的平衡。插入或删除节点后,若树不平衡,需要通过旋转操作(单旋转或双旋转)来恢复平衡。
AVL树的平衡因子 是该节点左子树的高度减去右子树的高度,平衡因子的绝对值不能大于1。
- 在AVL树中,任意节点的平衡因子只有
1或-1或0,因此AVL树也被称为高度平衡树。 - 对于每个节点,它的左子树和右子树的高度差不超过1。
- 这使得AVL树具有比普通的二叉搜索树更高的查询效率。
- 当插入或删除节点时,AVL树可以通过旋转操作来重新平衡树,从而保证其平衡性。
由于AVL树具有自平衡性,因此其最坏情况下的时间复杂度仅O(logn)。
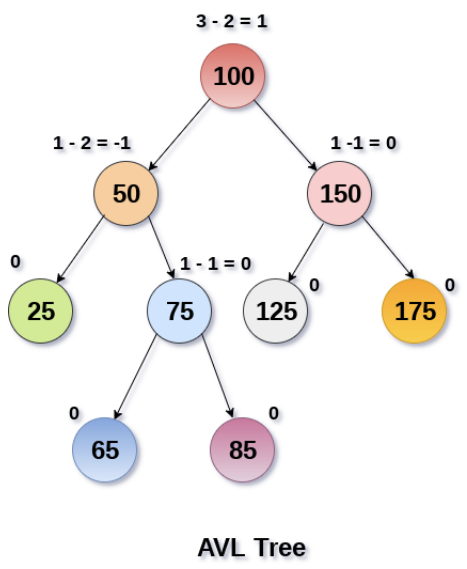
旋转操作
AVL树的插入和删除操作与普通的二叉搜索树类似,但是在插入或者删除之后,需要继续保持树的平衡。
- AVL树需要通过旋转操作来维护平衡。
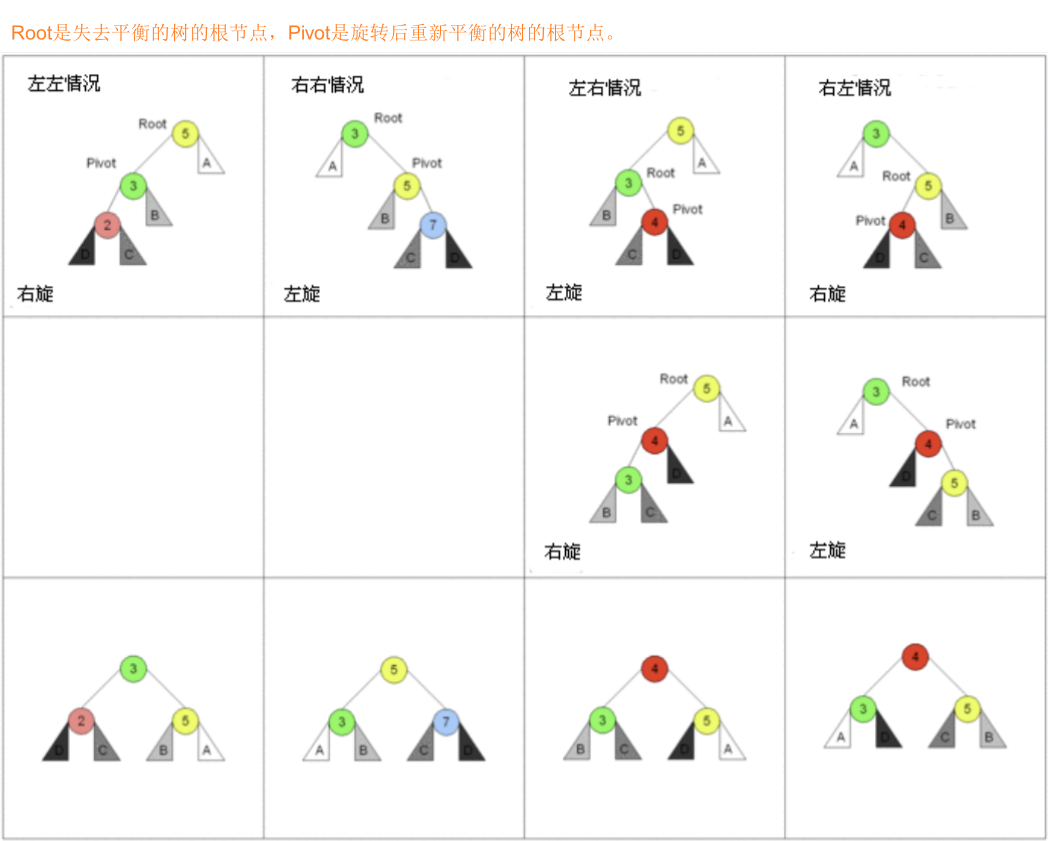
- 有四种情况旋转操作:左左情况、右右情况、左右情况和右左情况双旋。
- 具体使用哪一种旋转,要根据不同的情况来进行区分和判断。
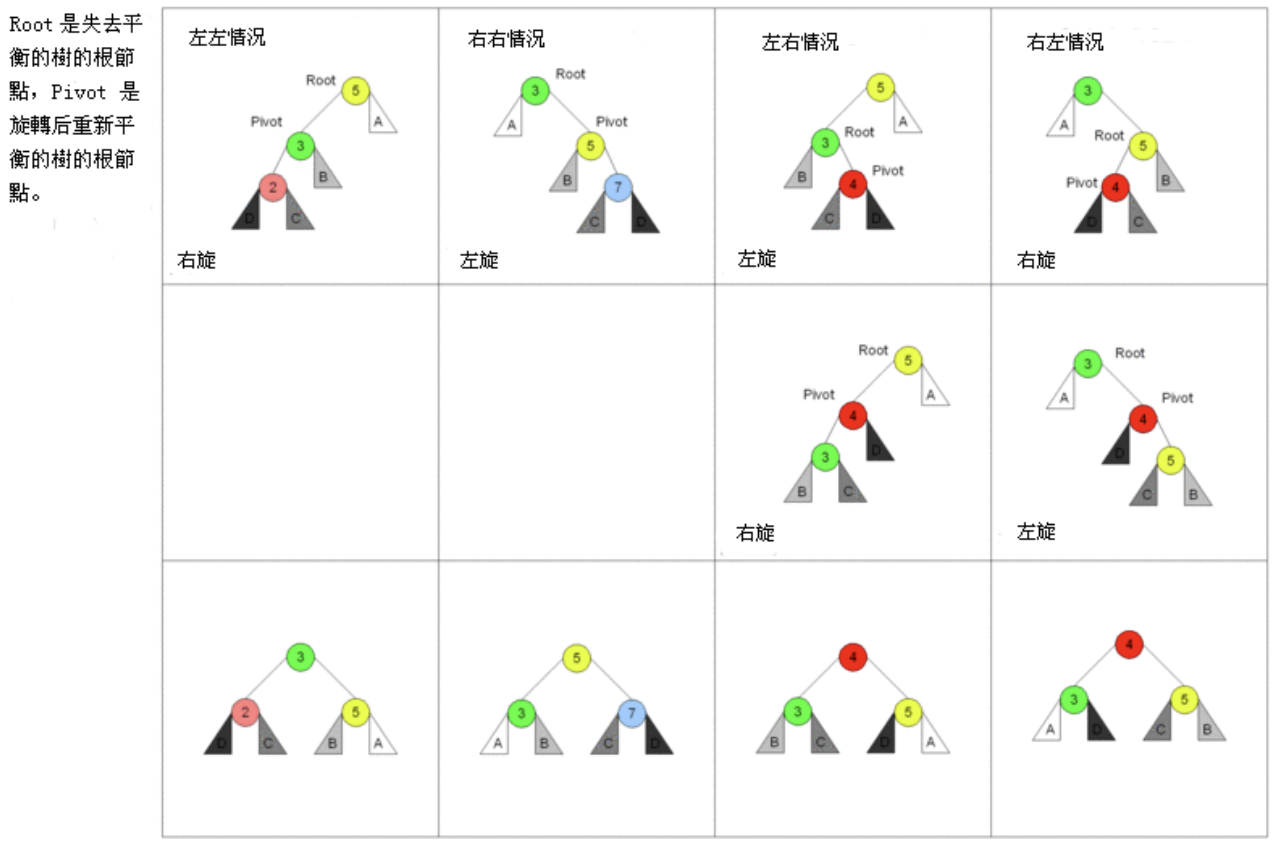
AVL树的实现
手写实现AVL树本身的过程是相当的复杂的,所以对于它的学习路线我进行了专门的设计。
我们如何学习呢?
- 步骤一:学习AVL树节点的封装。
- 步骤二:学习AVL树的旋转情况下如何编写代码。
- 步骤三:写出不同情况下进行的不同旋转操作。
- 步骤四:写出插入操作后,树的再平衡操作。
- 步骤五:写出删除操作后,树的再平衡操作。
我们可以通过分治的思想,一步步实现上面的功能,再将功能组合在一起就完成了AVL树的编写过程。
节点的封装
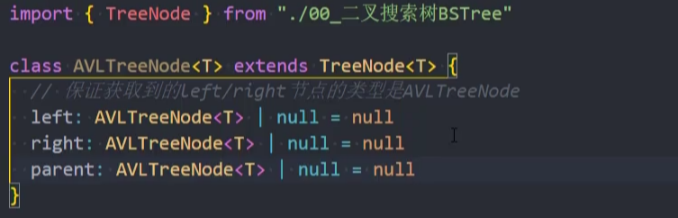
封装-AVLTreeNode
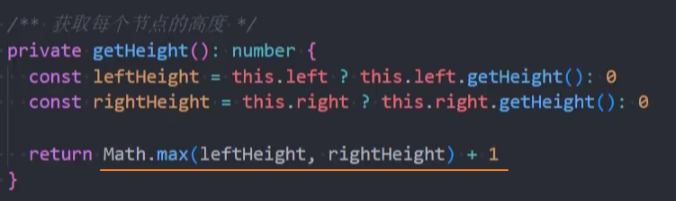
封装-getHeight()
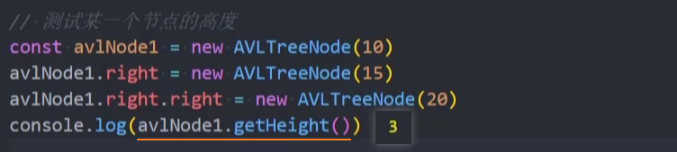
测试:
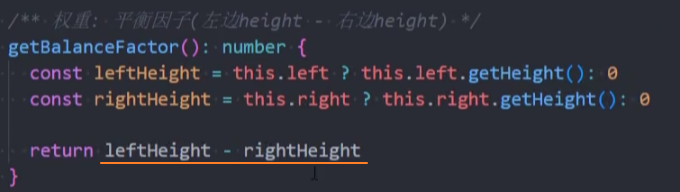
封装-getBalanceFactor()
测试:

封装-isBalanced
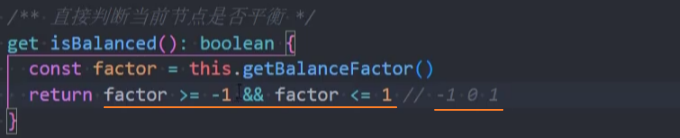
测试:

封装-higherChild
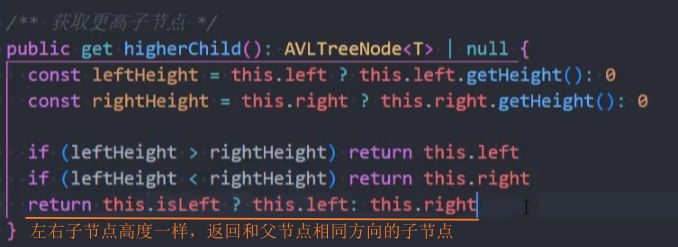
测试:

封装-旋转
封装-rightRotation()
实现步骤: 核心就是要修改变化节点的3个属性(指针):parent、left、right。
处理pivot节点:
- 1、
pivot = root.left:选择当前节点的左子节点作为旋转轴心。 - 2、
pivot.parent = root.parent:pivot的父节点指向root节点的父节点。
- 1、
处理pivot右子节点:
- 3、
root.left = pivot.right:root节点的左节点,指向pivot的右节点。 - 4、
pivot.right.parent = root:如果右节点有值, 那么右节点的父节点指向root节点。
- 3、
处理root节点:
- 5、
pivot.right = root:pivot的右节点指向root。 - 6、
root.parent = pivot:root节点的父节点指向pivot。
- 5、
挂载pivot节点:
- 7、
pivot.parent = null:如果pivot没有父节点,avltree.root = pivot。 - 8、
root.isLeft = true:如果pivot是父节点的左子节点,pivot.parent.left = pivot。 - 9、
root.isRight= true:如果pivot是父节点的右子节点,pivot.parent.right = pivot。
- 7、
图解:
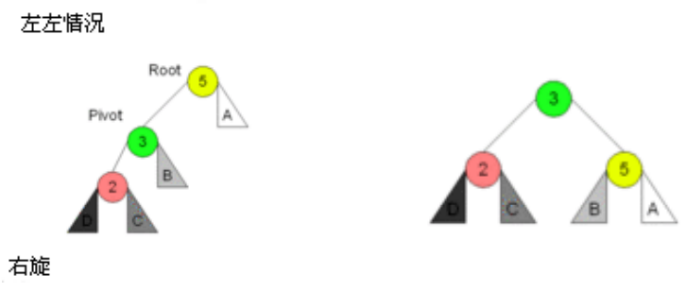
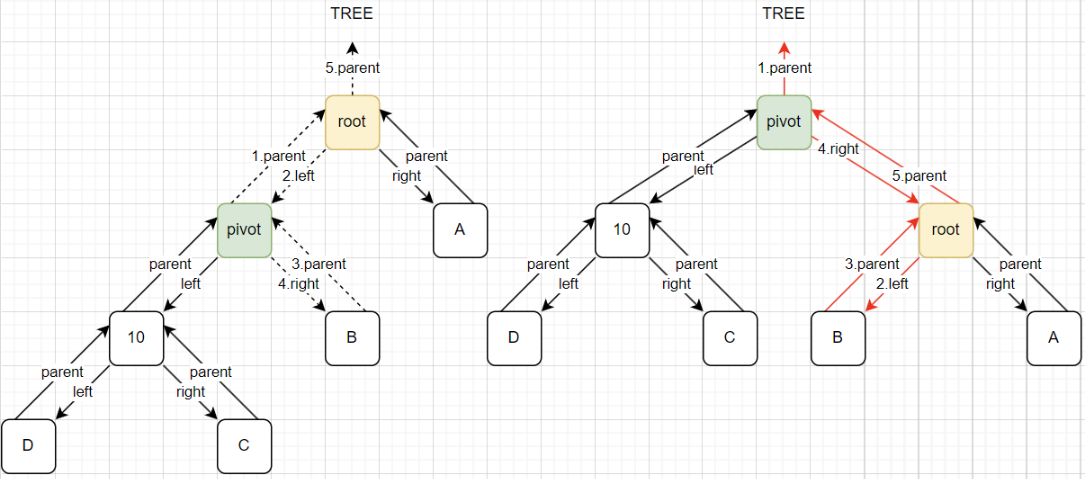
代码实现:
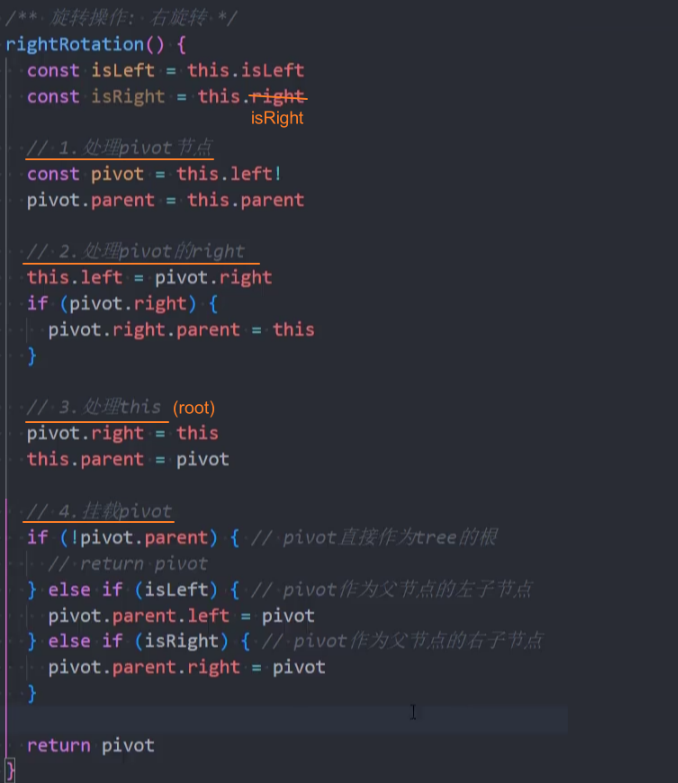
测试:
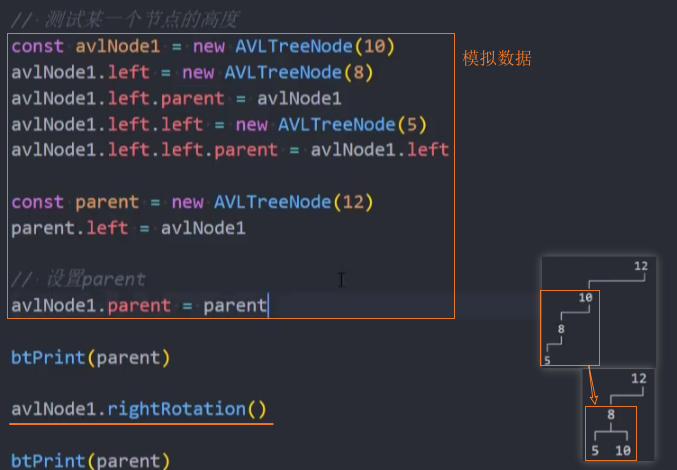
封装-leftRotation()
实现步骤: 核心就是要修改变化节点的3个属性(指针):parent、left、right。
- 处理pivot节点:
root.right- 1、
pivot = root.right:选择当前节点的右子节点作为旋转轴心。 - 2、
pivot.parent = root.parent:pivot的父节点指向root节点的父节点。
- 1、
- 处理pivot左子节点:
pivot.left- 3、
root.right = pivot.left:root节点的右子节点,指向pivot的左子节点。 - 4、
pivot.left.parent = root:如果左子节点有值, 那么左子节点的父节点指向root节点。
- 3、
- 处理root节点:
root(this)- 5、
pivot.left = root:pivot的左子节点指向root。 - 6、
root.parent = pivot:root节点的父节点指向pivot。
- 5、
- 挂载pivot节点:
pivot.parent- 7、
pivot.parent = null:如果pivot没有父节点,avltree.root = pivot。 - 8、
root.isLeft = true:如果pivot是父节点的左子节点,pivot.parent.left = pivot。 - 9、
root.isRight= true:如果pivot是父节点的右子节点,pivot.parent.right = pivot。
- 7、
图解:
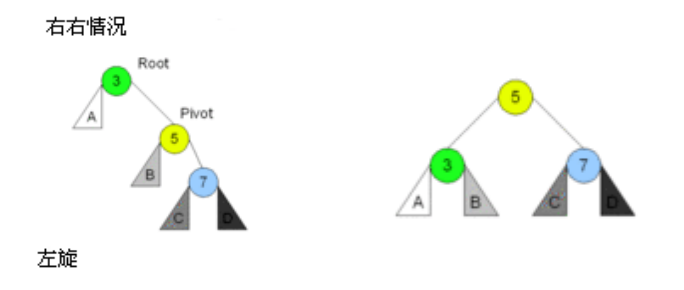
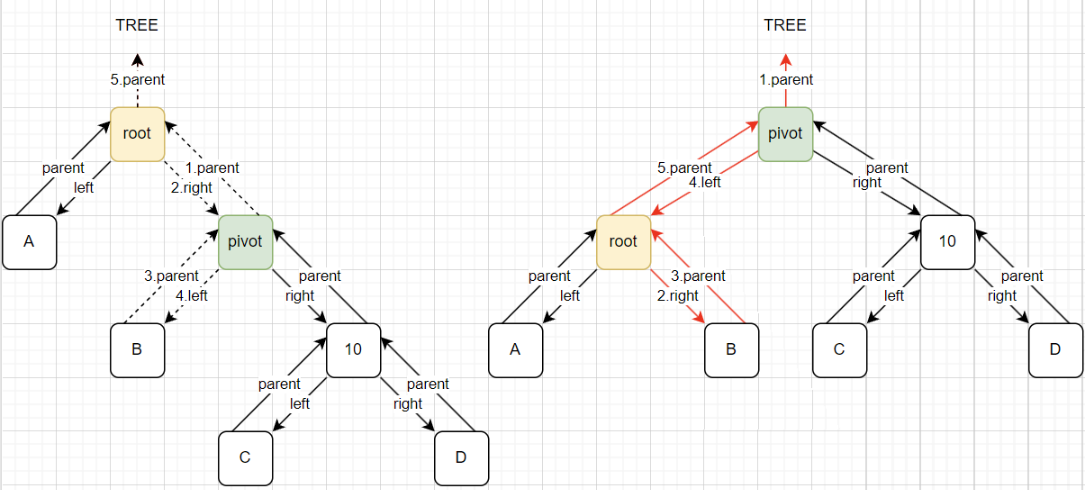
代码实现:
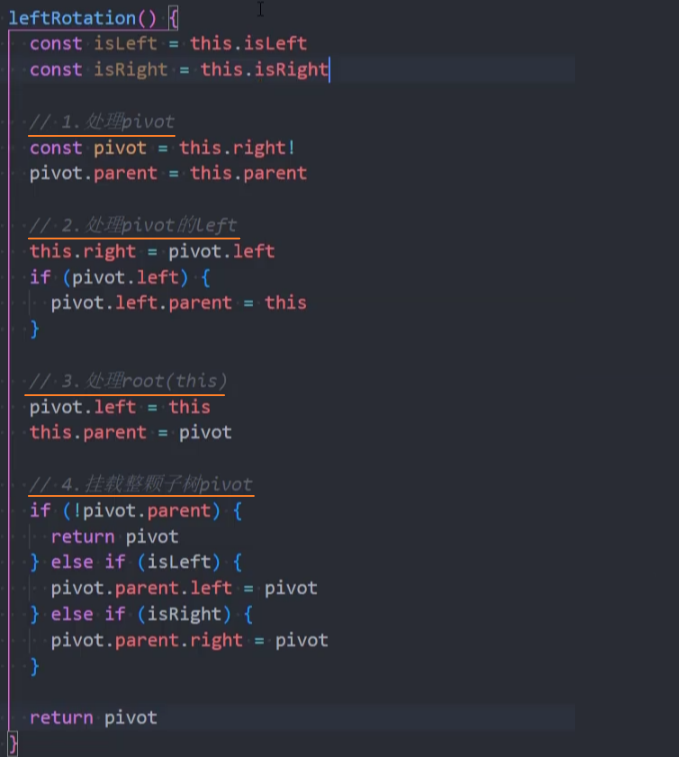
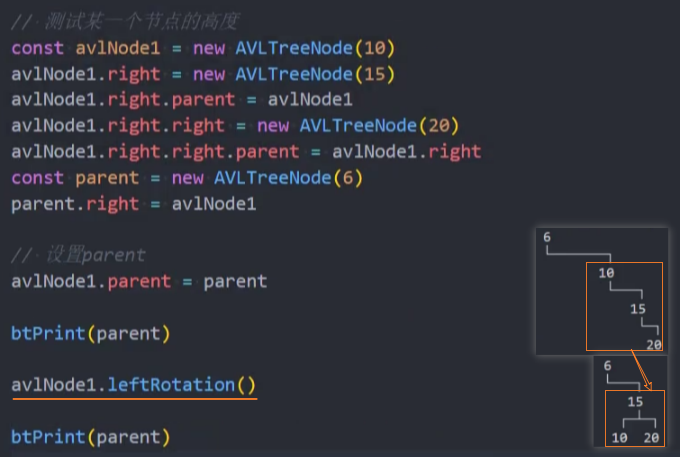
测试:
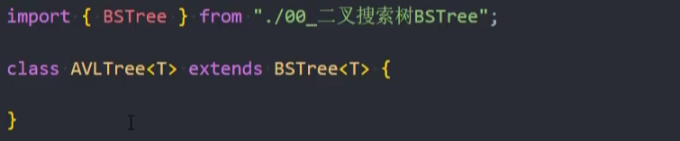
AVL树的封装
封装-AVLTree
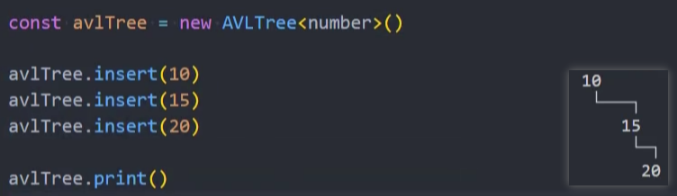
测试:
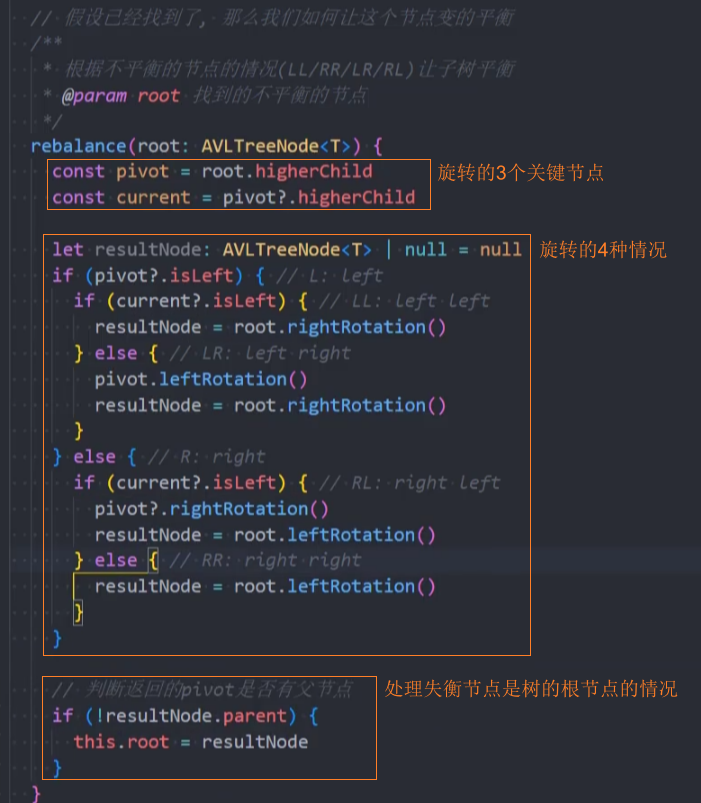
封装-rebalance()
思路:旋转的四种情况分析
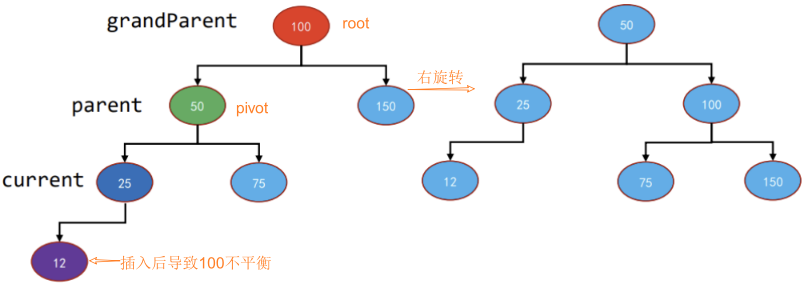
1、先找到失衡的节点:
- 失衡的节点称之为grandParent
- 失衡节点的儿子(更高的儿子)称之为parent
- 失衡节点的孙子(更高的孙子)称之为current
2、如果从grandParent到current的是:
- LL:左左情况,那么右旋转;
- RR:右右情况,那么左旋转;
- LR:左右情况,那么先对parent进行左旋转,再对grandParent进行右旋转;
- RL:右左情况,那么先对parent进行右旋转,再对grandParent进行左旋转;
图解:
代码实现:
封装-插入
图解:
封装-createNode()
需求:BSTree插入的节点类型 TreeNode,而AVLTree在insert()方法中需要创建一个AVLTreeNode。
思路:可以封装一个模板方法,让子类来进行重写即可。
代码实现:
1、在父类BSTree中封装createNode()方法
封装createNode()方法

修改父类
BSTree中的insert()方法
2、在子类AVLTree中重写createNode()方法
重写createNode()方法
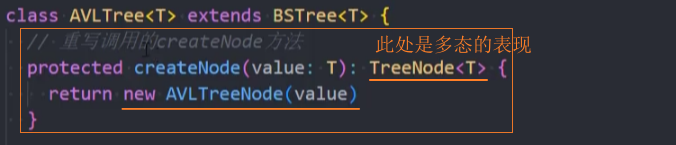
此时
AVLTree类实例调用父类中的insert()方法时,在该方法中调用createNode()创建的就是一个AVLTreeNode。
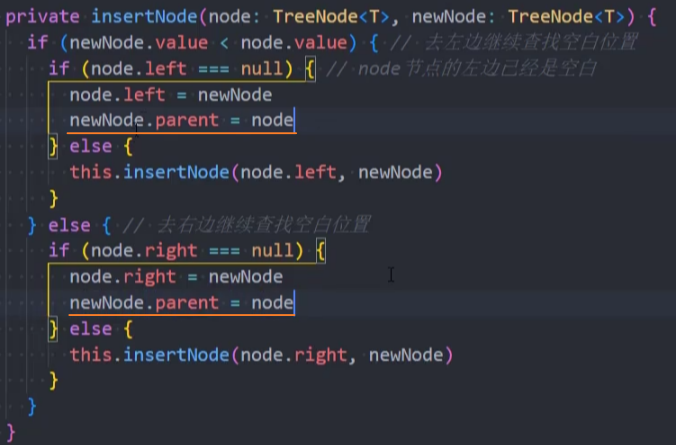
重构-insertNode()
需求:因为之后我们需要从当前节点中寻找parent节点,所以最好让每一个节点都保存一份parent节点。(之前代码是不需要的)
代码实现:
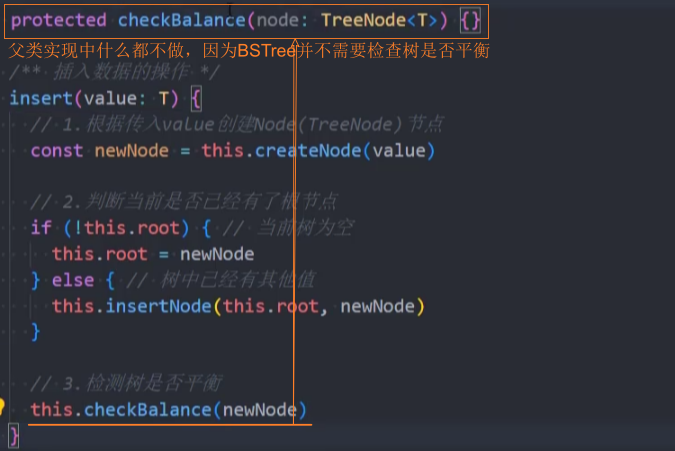
封装-checkBalance()
1、继续在父类BSTree中使用之前的insert()方法,在插入完成后调用checkBalance()去检查树的平衡
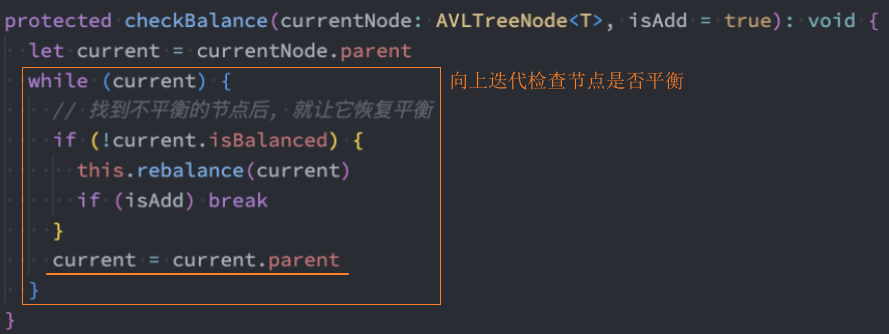
2、在子类AVLTree中重写父类的checkBalance()方法检查树的平衡
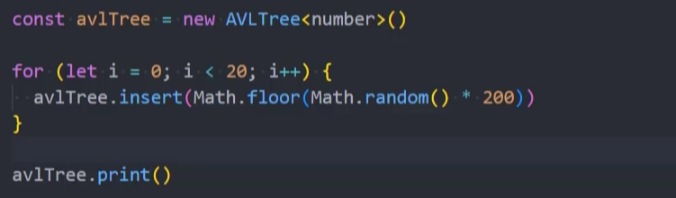
3、测试:随机一些数字,插入到AVLTree中来查看树是否平衡
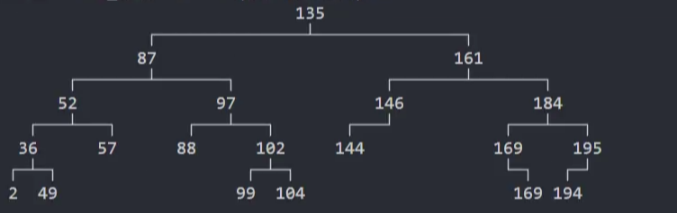
封装-删除@
图解:
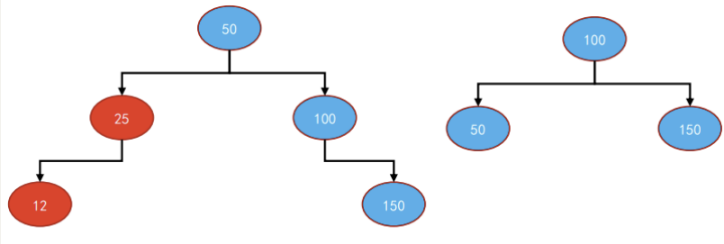
实现思路:
- 1、检查节点平衡:删除节点后,调用
checkBalance()检查节点是否平衡。 - 2、修改删除方案:
- 之前的方案是找到删除节点后,使用后继节点替换它。该方案需要处理的指针较多。
- 现在的方案是找到删除节点后,将后继节点的value赋值给它。再删除后继节点。
- 3、寻找删除节点(检测平衡的节点):
- 情况一:删除节点本身是叶子节点:删除节点 = current节点。
- 情况二:删除节点只有一个子节点:删除节点 = current节点。
- 情况三:删除节点有两个子节点:删除节点 = 后继节点原来的位置。
检查节点平衡
删除节点后,调用checkBalance()检查节点是否平衡
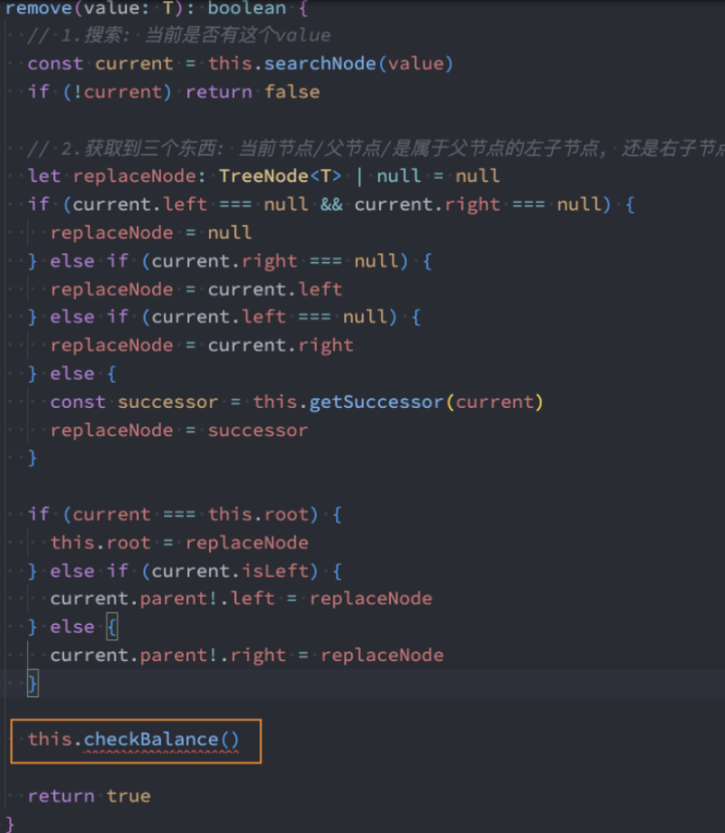
重构-remove()
checkBalance()中应该传入被删除的节点。但如果有两个子节点,找的就是前驱节点和后继节点,最终是将前驱和后继位置的节点删除掉。寻找的应该是从AVL树中被移除位置的节点。
情况一:删除节点本身是叶子节点:删除节点 = current节点。
情况二:删除节点只有一个子节点:删除节点 = current节点。
情况三:删除节点有两个子节点:删除节点 = 后继节点原来的位置。
关键点有两个:
- 必须要找到检测位置的节点
- 检测位置的节点必须有父节点
重构代码:使用第二种方案:找到删除节点后,将后继节点的value赋值给它。再删除后继节点。
1、重构-remove()方法
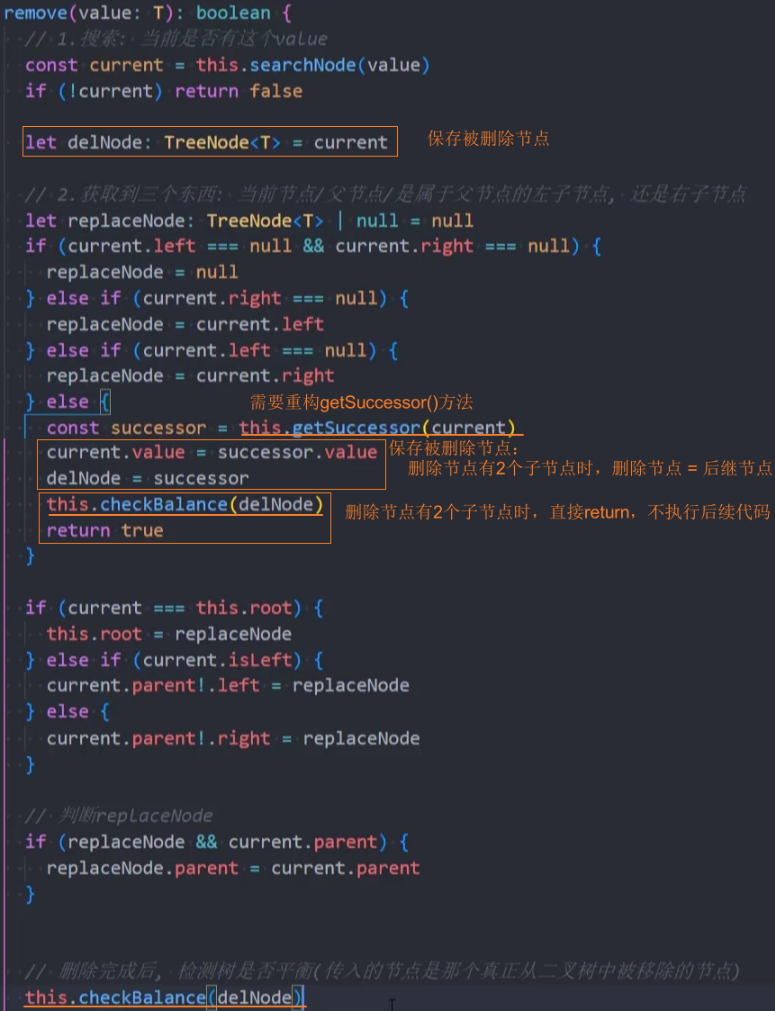
2、重构-getSuccessor()方法
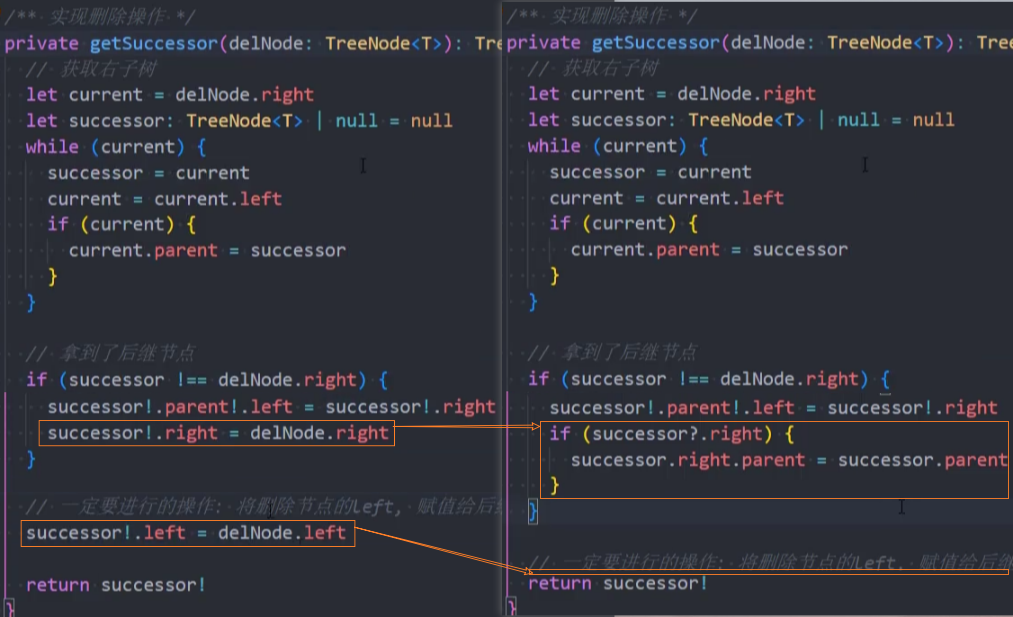
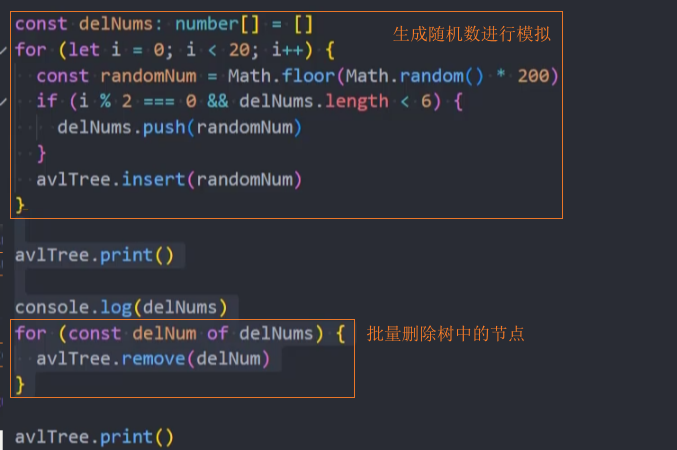
3、随机插入和删除测试
我们可以随机一些数字,插入,再删除,AVLTree中来查看树是否平衡。
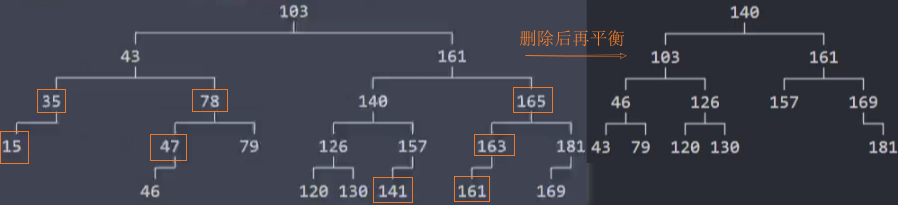
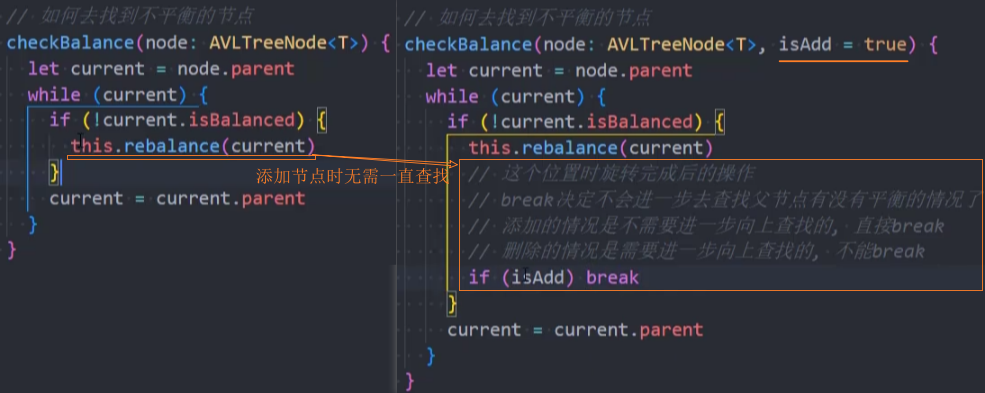
优化-rebalance()
执行rebalance()操作的节点:
- 插入节点的所有父节点:一直向上查找父节点。
- 删除节点的所有父节点:一直向上查找父节点。
继续rebalance()操作的前提: 取决于在插入或删除一个节点后后,是否改变了祖父节点的高度。
插入节点,再平衡rebalance后,高度不变,不需要继续后续节点的再平衡rebalance。
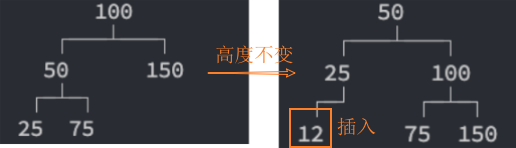
删除节点,再平衡rebalance后,高度改变了,需要继续后续节点的再平衡rebalance。
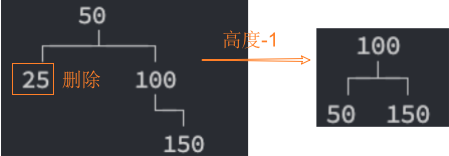
重构代码:
红黑树
概述
红黑树很难:红黑树是数据结构中很难的一个知识点,难到什么程度呢?
- 基本你跟别人聊数据结构的时候, 他不会和你聊红黑树, 因为它是数据结构中一个难点中的难点.
- 数据结构的学习本来就比较难了, 红黑树是又将难度上升一个档次的知识点.
面试段子:面试的时候经常出现这个场景:
- 面试官: 你知道红黑树吗?
- 面试者: 知道啊。
- 面试官: 知道原理吗?
- 面试者: 不知道啊。
- 面试官: 那你让‘不’过来面试我们公司吧,你先回去等通知吧。
面试:哪些面试会出现红黑树:
- 在面试时基本不会让手写红黑树,即使是面试Google、Apple这样的公司,也很少会出现。
- 通常是这样问题的(比如腾讯的一次面试题):为什么已经有平衡二叉树(比如AVL树)了,还需要红黑树。
红黑树
红黑树(Red-Black Tree) 是一种自平衡的二叉搜索树,它能够保证在最坏情况下,树的高度也不会超过 2 * log(n),从而使得基本的动态集合操作(如插入、删除、查找)能在对数时间内完成。
历史:
- 它在1972年由鲁道夫·贝尔发明,被称为“对称二叉B树”。
- 它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。
特性:红黑树除了符合二叉搜索树的基本规则外, 还添加了一些特性:
- 1、每个节点都是红色或黑色。
- 2、根节点是黑色。
- 3、每个叶子节点(NIL节点)是黑色的空节点。叶子节点通常是指代
null或者空指针的节点。- 因为在红黑树中,黑色节点的数量表示从根节点到叶子节点的黑色节点数量。
- 4、如果一个节点是红色的,那么它的子节点必须是黑色的。也就是说,红色节点不能有两个连续的红色节点。
- 它保证了红色节点的颜色不会影响树的平衡,同时保证了红色节点的出现不会导致连续的红色节点。
- 5、从任何一个节点到其所有后代叶子节点的路径上,经过的黑色节点数目相同。这意味着从根到每个叶子的路径上黑色节点的数量是相同的。
- 它是最重要的性质,保证了红黑树的平衡性。
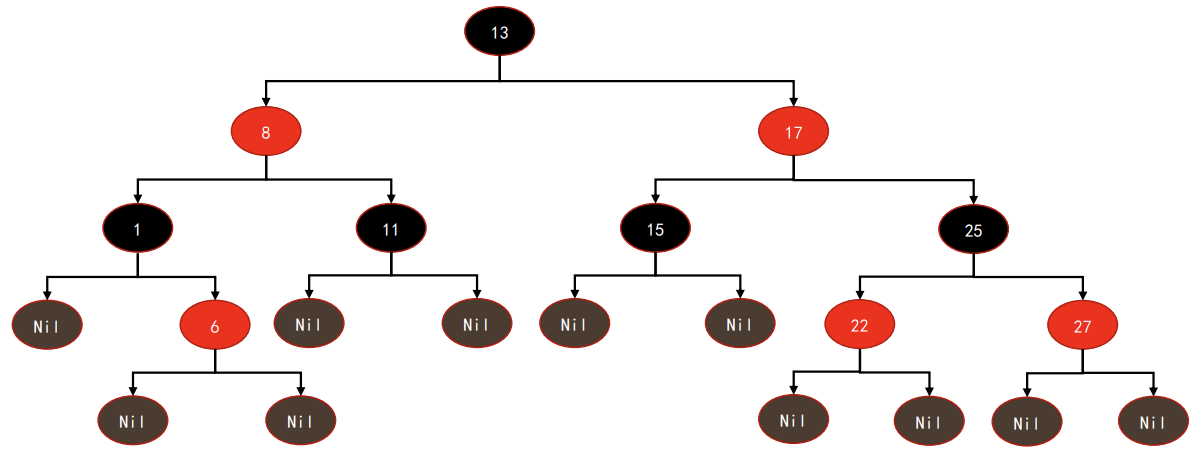
红黑树的相对平衡
前面的性质约束确保红黑树的关键特性:从根到叶子的最长可能路径, 不会超过最短可能路径的两倍长。结果就是这个树保持基本平衡。虽然没有做到绝对的平衡,但是可以保证在最坏的情况下依然是高效的。
如何确保最长路径不超过最短路径的两倍:
- 性质五:决定了最短路径和最长路径必须有相同的黑色节点。
- 最短路径:全部是黑色节点,黑色节点数量为
n。 - 最长路径:首尾是黑色节点,黑色节点数量为
n;中间全部是红色节点,红色节点数量为n – 1。- 性质二:根节点是黑节点。
- 性质三:叶子节点都是黑节。
- 性质四:两个红色节点不能相连。
- 最短路径边的数量:
n – 1。 - 最长路径边的数量:
(n + n – 1) - 1 = 2n – 2。 - 最长路径一定不超过最短路径的2倍:
2n-2 = 2 * (n-1)。
对比AVL树的性能
性能对比:
AVL树是一种平衡度更高的二叉搜索树,所以在搜索效率上会更高。但AVL树为了维护这种平衡性,在插入和删除操作时,通常会进行更多的旋转操作,所以效率相对红黑树较低。它们的搜索、添加、删除时间复杂度都是O(logn),但是细节上会有一些差异。
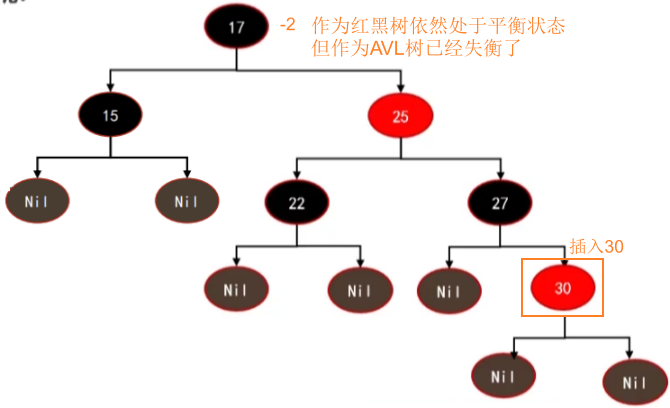
插入:AVL树 < 红黑树
- 插入红黑树:向红黑树插入30,会被插入到27的右子节点,并且30是红色节点时,依然符合红黑树的性质。对于红黑树来说,它不需要进行任何平衡操作。
- 插入AVL树:向AVL树插入30,也会被插入到27的右子节点,此时17节点会失衡。必须对17、25、27节点进行左旋转操作。
删除:AVL树 < 红黑树
搜索:红黑树 < AVL树
- 红黑树的高度比AVL树要高,同样是搜索30,红黑树需要搜索4次,AVL树搜索3次。
总结:红黑树相当于牺牲了一点点的搜索性能,来提高了插入和删除的性能。
开发中如何选择:
选择AVL树还是红黑树,取决于具体的应用需求。
如果需要保证每个节点的高度尽可能地平衡,可以选择AVL树。
如果需要保证删除操作的效率,可以选择红黑树。
在早期的时候,很多场景会选择AVL树,目前选择红黑树的越来越多(AVL树依然是一种重要的平衡树)。
比如操作系统内核中的内存管理;
比如Java的TreeMap、TreeSet底层的源码;
红黑树的实现
实现步骤分析
实现一个 TypeScript 红黑树的详细步骤:
- 定义红黑树的节点:定义一个带有键、值、颜色、左子节点、右子节点和父节点的类;
- 实现左旋操作:将一个节点向左旋转,保持红黑树的性质;
- 实现右旋操作:将一个节点向右旋转,保持红黑树的性质;
- 实现插入操作:在红黑树中插入一个新的节点,并保持红黑树的性质;
- 实现删除操作:从红黑树中删除一个节点,并保持红黑树的性质;
- 实现修复红黑树性质:在插入或删除操作后,通过旋转和变色来修复红黑树的性质;
- 其他方法较为简单,可以自行实现;
RedBlackNode
使用 TypeScript 的泛型编写红黑树的节点。
enum Color {
RED,
BLACK,
}
class RedBlackNode<T> {
value: T;
color: Color;
parent: RedBlackNode<T> | null;
left: RedBlackNode<T> | null;
right: RedBlackNode<T> | null;
constructor(
value: T,
color: Color = Color.RED,
parent: RedBlackNode<T> | null = null,
left: RedBlackNode<T> | null = null,
right: RedBlackNode<T> | null = null
) {
this.value = value;
this.color = color;
this.parent = parent;
this.left = left;
this.right = right;
}
}RedBlackTree
红黑树的整体结构:
class RedBlackTree<T> {
root: RedBlackNode<T> | null = null;
// 查找某个节点再红黑树中的最小值
minimum(node: RedBlackNode<T> | null = this.root): RedBlackNode<T> | null {
let current = node;
while (current && current.left) {
current = current.left;
}
return current;
}
// 查找红黑树中的某个节点
private search(value: T): RedBlackNode<T> | null {
let node = this.root;
let parent: RedBlackNode<T> | null = null;
while (node) {
if (node.value === value) {
node.parent = parent;
return node;
}
parent = node;
if (value < node.value) {
node = node.left;
} else {
node = node.right;
}
}
return null;
}
}
export {};旋转操作
实现左旋转和有旋转操作:
/**
* 左旋操作
*
* @param node 要进行左旋的结点
*/
private leftRotate(node: RedBlackNode<T>) {
// 获取 node 的右子节点
let rightChild = node.right!;
// 将右子节点的左子节点赋值给 node 的右子节点
node.right = rightChild.left;
// 如果右子节点的左子节点不为空,则将右子节点的左子节点的父节点指向 node
if (rightChild.left) {
rightChild.left.parent = node;
}
// 将右子节点的父节点指向 node 的父节点
rightChild.parent = node.parent;
// 如果 node 的父节点为空,则将右子节点设为根结点
if (!node.parent) {
this.root = rightChild;
}
// 如果 node 是它父节点的左子节点,则将右子节点设为 node 父节点的左子节点
else if (node === node.parent.left) {
node.parent.left = rightChild;
}
// 否则,将右子节点设为 node 父节点的右子节点
else {
node.parent.right = rightChild;
}
// 将 node 的父节点指向 rightChild,并将 rightChild 的左子节点指向 node
rightChild.left = node;
node.parent = rightChild;
}
/**
* 右旋转
* @param node 旋转节点
*/
private rightRotate(node: RedBlackNode<T>) {
// 获取旋转节点的左子节点
let leftChild = node.left!;
// 将旋转节点的左子节点的右子节点,接到旋转节点的左边
node.left = leftChild.right;
// 如果左子节点的右子节点不为空,设置它的父节点为旋转节点
if (leftChild.right) {
leftChild.right.parent = node;
}
// 将左子节点的父节点设为旋转节点的父节点
leftChild.parent = node.parent;
// 如果旋转节点的父节点不存在,说明左子节点变成根节点
if (!node.parent) {
this.root = leftChild;
} else if (node === node.parent.right) {
// 如果旋转节点是它父节点的右子节点,将父节点的右子节点设为左子节点
node.parent.right = leftChild;
} else {
// 如果旋转节点是它父节点的左子节点,将父节点的左子节点设为左子节点
node.parent.left = leftChild;
}
// 将旋转节点设为左子节点的右子节点
leftChild.right = node;
// 将旋转节点的父节点设为左子节点
node.parent = leftChild;
}插入操作
实现插入操作,并且插入后实现红黑树的平衡和保持性质:
insert(value: T) {
// 创建一个新节点
let newNode = new RedBlackNode(value);
// 如果红黑树为空,将该节点作为根节点
if (!this.root) {
this.root = newNode;
// 根节点为黑色
newNode.color = Color.BLACK;
return;
}
// 初始化搜索变量current和parent
let current: RedBlackNode<T> | null = this.root;
let parent: RedBlackNode<T> | null = null;
// 搜索合适的插入位置
while (current) {
parent = current;
// 如果value小于当前节点,则继续往左子树搜索
if (value < current.value) {
current = current.left;
// 否则继续往右子树搜索
} else {
current = current.right;
}
}
// 将新节点的父节点设置为搜索到的父节点
newNode.parent = parent;
// 将新节点插入到合适的位置
if (value < parent!.value) {
parent!.left = newNode;
} else {
parent!.right = newNode;
}
// 修复插入导致的红黑树性质破坏
this.fixInsertion(newNode);
}
private fixInsertion(node: RedBlackNode<T>) {
// 当父节点存在且颜色为红时
while (node.parent && node.parent.color === Color.RED) {
// 获取祖父节点
let grandParent = node.parent.parent!;
// 父节点是祖父节点的左子节点
if (node.parent === grandParent.left) {
// 获取叔叔节点
let uncle = grandParent.right;
// 叔叔节点存在且颜色为红
if (uncle && uncle.color === Color.RED) {
// 将父节点颜色改为黑,叔叔节点颜色改为黑,祖父节点颜色改为红,node节点变为祖父节点,继续循环
node.parent.color = Color.BLACK;
uncle.color = Color.BLACK;
grandParent.color = Color.RED;
node = grandParent;
} else {
// 当前节点是父节点的右子节点
if (node === node.parent.right) {
// 将当前节点变为父节点,进行左旋操作
node = node.parent;
this.leftRotate(node);
}
// 将父节点颜色改为黑,祖父节点颜色改为红,进行右旋操作
node.parent!.color = Color.BLACK;
grandParent.color = Color.RED;
this.rightRotate(grandParent);
}
} else {
// 父节点是祖父节点的右子节点,与上面的同理
let uncle = grandParent.left;
// 如果叔叔节点是红色的
if (uncle && uncle.color === Color.RED) {
// 父节点设置为黑色
node.parent.color = Color.BLACK;
// 叔叔节点设置为黑色
uncle.color = Color.BLACK;
// 祖父节点设置为红色
grandParent.color = Color.RED;
// 将当前节点设置为祖父节点
node = grandParent;
} else {
// 如果当前节点是父节点的左节点
if (node === node.parent.left) {
// 将当前节点设置为父节点
node = node.parent;
// 右旋父节点
this.rightRotate(node);
}
// 父节点设置为黑色
node.parent!.color = Color.BLACK;
// 祖父节点设置为红色
grandParent.color = Color.RED;
// 左旋祖父节点
this.leftRotate(grandParent);
}
}
}
// 根节点设置为黑色节点
this.root!.color = Color.BLACK;
}删除操作
红黑树的删除操作和删除后的再平衡
/**
* 删除红黑树中的某个节点
*
* @param value 要删除的节点的值
*/
delete(value: T) {
// 先找到要删除的节点
const nodeToDelete = this.search(value);
// 如果不存在,就直接退出
if (!nodeToDelete) {
return;
}
// 否则删除节点
this._delete(nodeToDelete);
}
/**
* 删除红黑树中的节点
* @param node 要删除的节点
*/
private _delete(node: RedBlackNode<T>) {
// 如果该节点同时存在左右节点,则找到右子树的最小节点作为该节点的后继
if (node.left && node.right) {
const successor = this.minimum(node.right);
node.value = successor!.value;
node = successor!;
}
let child: RedBlackNode<T> | null;
// 如果该节点存在左节点,则将该左节点作为它的唯一子节点
if (node.left) {
child = node.left;
} else if (node.right) {
// 如果该节点存在右节点,则将该右节点作为它的唯一子节点
child = node.right;
} else {
child = null;
}
// 如果该节点没有子节点,直接删除
if (!child) {
// 如果该节点是黑色,则需要特殊处理
if (node.color === Color.BLACK) {
this._deleteCase1(node);
}
this._removeNode(node);
} else {
// 如果该节点是黑色,则需要特殊处理
if (node.color === Color.BLACK) {
// 如果该节点的唯一子节点是红色,则将该唯一子节点设置为黑色
if (child.color === Color.RED) {
child.color = Color.BLACK;
} else {
this._deleteCase1(node);
}
}
// 用该节点的唯一子节点替换该节点
this._replaceNode(node, child);
}
}
private _deleteCase1(node: RedBlackNode<T>) {
// 如果有父节点,就进入 Case 2
if (node.parent) {
this._deleteCase2(node);
}
}
private _deleteCase2(node: RedBlackNode<T>) {
// 找到兄弟节点
const sibling = this._sibling(node);
// 如果兄弟节点存在且颜色为红色
if (sibling && sibling.color === Color.RED) {
// 父节点颜色变为红色
node.parent!.color = Color.RED;
// 兄弟节点颜色变为黑色
sibling.color = Color.BLACK;
// 如果删除的节点是左子节点
if (node === node.parent!.left) {
// 则向左旋转
this.leftRotate(node.parent!);
} else {
// 否则向右旋转
this.rightRotate(node.parent!);
}
}
this._deleteCase3(node);
}
private _deleteCase3(node: RedBlackNode<T>) {
const sibling = this._sibling(node);
// 当父节点颜色是黑色,兄弟节点颜色是黑色,兄弟节点的左右子节点都是黑色
if (
node.parent!.color === Color.BLACK &&
sibling &&
sibling.color === Color.BLACK &&
(!sibling.left || sibling.left.color === Color.BLACK) &&
(!sibling.right || sibling.right.color === Color.BLACK)
) {
// 将兄弟节点颜色设置为红色
sibling.color = Color.RED;
// 递归处理父节点
this._deleteCase1(node.parent!);
} else {
// 进入下一个情况
this._deleteCase4(node);
}
}
private _deleteCase4(node: RedBlackNode<T>) {
const sibling = this._sibling(node);
// 当父节点为红色,兄弟节点为黑色,且兄弟节点的左右子树为黑色时
if (
node.parent!.color === Color.RED &&
sibling &&
sibling.color === Color.BLACK &&
(!sibling.left || sibling.left.color === Color.BLACK) &&
(!sibling.right || sibling.right.color === Color.BLACK)
) {
// 将兄弟节点涂红色
sibling.color = Color.RED;
// 父节点涂黑色
node.parent!.color = Color.BLACK;
} else {
// 否则进入下一个删除 case
this._deleteCase5(node);
}
}
private _deleteCase5(node: RedBlackNode<T>) {
const sibling = this._sibling(node);
if (sibling && sibling.color === Color.BLACK) {
// 如果当前节点是它父的左节点,并且兄弟节点的右节点存在且为红色
if (
node === node.parent!.left &&
sibling.right &&
sibling.right.color === Color.RED
) {
// 将兄弟节点的颜色设置为红色
sibling.color = Color.RED;
// 兄弟节点的右节点设置为黑色
sibling.right!.color = Color.BLACK;
// 对兄弟节点进行左旋
this.leftRotate(sibling);
} else if (
node === node.parent!.right &&
sibling.left &&
sibling.left.color === Color.RED
) {
// 同上
sibling.color = Color.RED;
sibling.left!.color = Color.BLACK;
this.rightRotate(sibling);
}
}
this._deleteCase6(node);
}
private _deleteCase6(node: RedBlackNode<T>) {
const sibling = this._sibling(node);
// 将兄弟节点颜色设置成父节点颜色
sibling!.color = node.parent!.color;
// 将父节点颜色设置成黑色
node.parent!.color = Color.BLACK;
if (node === node.parent!.left) {
// 将兄弟节点的右子节点颜色设置成黑色
sibling!.right!.color = Color.BLACK;
// 对父节点左旋
this.leftRotate(node.parent!);
} else {
// 将兄弟节点的左子节点颜色设置成黑色
sibling!.left!.color = Color.BLACK;
// 对父节点右旋
this.rightRotate(node.parent!);
}
}
private _removeNode(node: RedBlackNode<T>) {
if (!node.parent) {
this.root = null;
} else if (node === node.parent.left) {
node.parent.left = null;
} else {
node.parent.right = null;
}
}
private _replaceNode(oldNode: RedBlackNode<T>, newNode: RedBlackNode<T>) {
if (!oldNode.parent) {
this.root = newNode;
} else if (oldNode === oldNode.parent.left) {
oldNode.parent.left = newNode;
} else {
oldNode.parent.right = newNode;
}
newNode.parent = oldNode.parent;
}
private _sibling(node: RedBlackNode<T>) {
if (!node.parent) {
return null;
}
return node === node.parent.left ? node.parent.right : node.parent.left;
}